Doctoral students in my group Top

I co-supervise Ph.D. students with the Cavendish Astrophysics Group, with weekly meetings.

Student supervision Gantt chart showing project timelines and milestones - hover to enlarge

Postdoctoral job-seeking Top

General Advice Top

This section provides essential guidance for securing postdoctoral positions in theoretical physics, cosmology, and high-energy physics. Content generated with assistance from AI advisory systems.

Loading postdoctoral career advice...

A Note About Online Forums

You may encounter unofficial online forums, often called the "postdoc rumour mill," where applicants anonymously share updates about applications, interviews, and decisions. While these platforms can provide a sense of community and market awareness, they come with significant drawbacks worth considering. The information is unverified and often incomplete, which can lead to unnecessary anxiety when comparing your timeline to others. Many students find that frequent checking becomes counterproductive, creating stress rather than helpful insights. If you choose to use such forums, consider setting clear boundaries—perhaps a brief check once or twice weekly rather than daily monitoring. Focus on what you can control: your applications, your research, and maintaining your wellbeing throughout the process.

Academic Job Boards Top

The following platforms are essential resources for finding postdoctoral positions and fellowships in theoretical physics and related fields:

INSPIRE-HEP Jobs

The primary job listing platform for high-energy physics, cosmology, and theoretical physics. Features positions worldwide with detailed categories and search filters.

Visit INSPIRE-HEP Jobs
API Available

Loading latest postdoc positions from INSPIRE-HEP...

Academic Jobs Online

Comprehensive academic job board covering multiple disciplines including physics and astronomy. Features detailed application tracking and institution profiles.

Visit Academic Jobs Online
No Public API

Important: Most physics and astronomy departments use AJO as their primary application portal. You apply through AJO rather than directly to institutions.

AAS Job Register

The American Astronomical Society's job listing platform, focusing on astronomy and astrophysics positions including postdocs and fellowships.

Visit AAS Job Register
No Public API

Note: This platform does not provide a public API. Manual browsing recommended for astronomy-related positions.

Euraxess

European research career platform featuring postdoc and research positions across Europe. Particularly strong for EU-funded research positions.

Visit Euraxess
XML API (Contact Required)

API Status: Euraxess provides XML-based APIs for job submissions, but requires contacting support@euraxess.org for access credentials.

Interfolio Dossier

Essential document management platform for academic job applications. Handles confidential reference letters, CV storage, and application materials organization.

Visit Interfolio Dossier
Document Management Service

US Essential: Many American universities require applications through Interfolio. Critical for managing confidential reference letters from multiple recommenders.

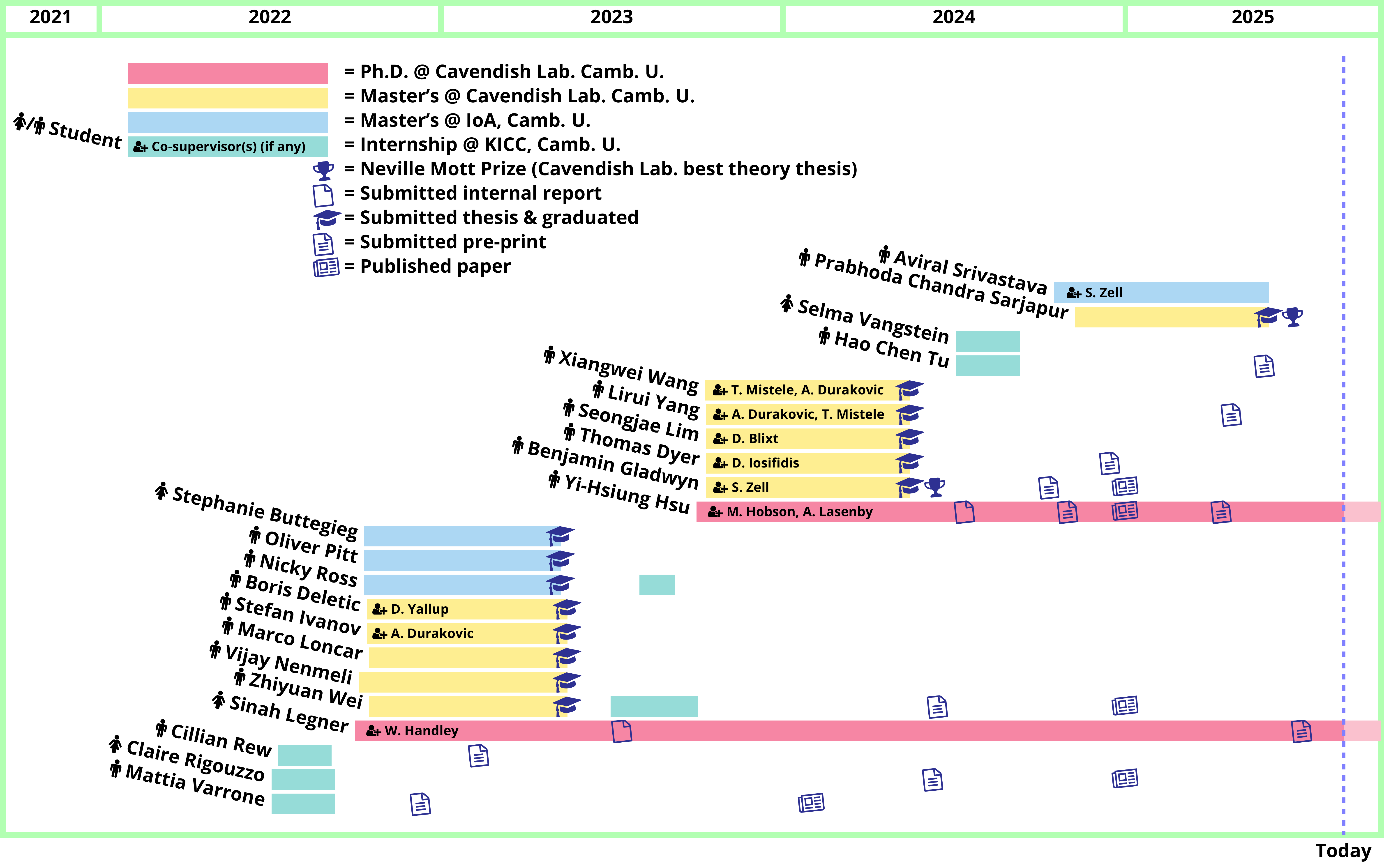
Current Ph.D. Students Top

Weekly meetings Top

Cavendish Gravity
Join Meeting
Link: meet.google.com/qew-mvfw-dkg
Cavendish Gravity
Join Meeting
ID: TBD
Password: TBD

Miscellaneous materials Top

Regarding the Schwarzschild chart for Arthur, I believe that the following snippet should parse:

<<xAct`xPlain`;

Comment@"Define some functions that will parameterise our line element.";

DefScalarFunction[B1,PrintAs->"\[CapitalTheta]"];
DefScalarFunction[B2,PrintAs->"\[CapitalOmega]"];

Comment@"Define the chart for spherical polar coordinates.";

DefChart[SphericalPolar,M4,{0,1,2,3},{ct[],cr[],ctheta[],cphi[]},ChartColor->Green];

PrintAs@ct^="\[ScriptT]";
PrintAs@cr^="\[ScriptR]";
PrintAs@ctheta^="\[Theta]";
PrintAs@cphi^="\[Phi]";

Comment@"Set the components of the metric.";

MatrixForm[MatrixSphericalPolar=DiagonalMatrix[{B1[cr[]]^2,-B2[cr[]]^2,-cr[]^2,-cr[]^2*Sin[ctheta[]]^2}]];
MatrixForm@MetricInBasis[G,-SphericalPolar,MatrixSphericalPolar];
MetricCompute[G,SphericalPolar,All,Verbose->False];

The key point is that you can’t define a chart with xTensor, because xTensor is purely abstract and has not functionality for explicit coordinate functions. That is the whole point of xCoba. You can grab the xPlain package from my GitHub page, and note that my choice of metric symbol and Penrose slots may differ from yours.

Speaking of differences in defined symbols, I make a point of using Pascal case for Wolfram Language computations as far as possible. For this reason, my metric is usually G, and I tend to allocate all the lower-case letters to abstract indices with the Alphabet[] command. For example, this snippet is part of my basic setup:

(*===============*)
(*  DefManifold  *)
(*===============*)

Comment@"We will define a manifold.";
DefManifold[M4,4,IndexRange[{a,z}]];

Comment@"We will define a metric and covariant derivative.";
GSymb="\[ScriptG]";
DefMetric[-1,G[-a,-b],CD,{";","\!\(\*OverscriptBox[\(\[Del]\), \(\[SmallCircle]\)]\)"},PrintAs->GSymb,SymCovDQ->True];

(*-----------------------------------------------------------------------*)
(*  Relabeling of the indices so that we can type Roman and look Greek!  *)
(*-----------------------------------------------------------------------*)

StandardIndices=ToString/@Alphabet[];

GeoStandardIndicesSymb=(ToString@#)&/@Evaluate@((#[[2]])&/@{
	{a,"\[Alpha]"},
	{b,"\[Beta]"},
	{c,"\[Chi]"},
	{d,"\[Delta]"},
	{e,"\[Epsilon]"},
	{f,"\[Phi]"},
	{g,"\[Gamma]"},
	{h,"\[Eta]"},
	{i,"\[Iota]"},
	{j,"\[Theta]"},
	{k,"\[Kappa]"},
	{l,"\[Lambda]"},
	{m,"\[Mu]"},
	{n,"\[Nu]"},
	{o,"\[Omicron]"},
	{p,"\[Pi]"},
	{q,"\[Omega]"},
	{r,"\[Rho]"},
	{s,"\[Sigma]"},
	{t,"\[Tau]"},
	{u,"\[Upsilon]"},
	{v,"\[Psi]"},
	{w,"\[Omega]"},
	{x,"\[Xi]"},
	{y,"\[CurlyPhi]"},
	{z,"\[Zeta]"}});

(PrintAs@Evaluate@#1^=Evaluate@#2)&~MapThread~{ToExpression/@StandardIndices,GeoStandardIndicesSymb};

For the example sent by Arthur, g is used instead of G, and only limited indices are available. In this case I think this will work:

MatrixForm@MetricInBasis[g,-SphericalPolar,MatrixSphericalPolar];
MetricCompute[g,SphericalPolar,All,Verbose->False];

Extracting components from the field equations Top

Let’s first check that the metric defined was what we wanted:

Comment@"Just to check the line element which we built here, let's have a look!";

Expr=G[{-a,-SphericalPolar},{-b,-SphericalPolar}];
DisplayExpression@Expr;
Expr//=ComponentArray;
DisplayExpression@MatrixForm@Expr;
Expr//=ToValues;
DisplayExpression@MatrixForm@Expr;

Comment@"Now how about the inverse metric?";

Expr=G[{a,SphericalPolar},{b,SphericalPolar}];
DisplayExpression@Expr;
Expr//=ComponentArray;
DisplayExpression@MatrixForm@Expr;
Expr//=ToValues;
DisplayExpression@MatrixForm@Expr;

Assuming we're happy with that, we can also define some scalar fields: 

DefTensor[Phi[],M4,PrintAs->"\[Phi]"];
DefTensor[Psi[],M4,PrintAs->"\[Psi]"];

DefScalarFunction[Psis,PrintAs->"\[Psi]"];
DefScalarFunction[Phis,PrintAs->"\[Phi]"];

We can introduce a useful function for moving to the Schwarzschild-like chart:

RawSchwarzschildLike[Expr_]:=Module[{SchwarzschildLikeExpr=Expr},
	SchwarzschildLikeExpr//=NoScalar;	
	SchwarzschildLikeExpr=SchwarzschildLikeExpr/.{
		Phi[]->Phis[cr[]],
		Psi[]->Psis[cr[]]
		};	
	SchwarzschildLikeExpr//=ToBasis[SphericalPolar];
	SchwarzschildLikeExpr//=TraceBasisDummy;
	SchwarzschildLikeExpr//=ToValues;
	SchwarzschildLikeExpr//=ToValues;

	(*----------------------------------------*)
	(*  Evaluate at the equator of the chart  *)
	(*----------------------------------------*)

	SchwarzschildLikeExpr=SchwarzschildLikeExpr/.{ctheta[]->Pi/2};

	(*--------------------------------------------------------------------*)
	(*  Now that variations are done, we reveal the square root function  *)
	(*--------------------------------------------------------------------*)

	SchwarzschildLikeExpr];

ToSchwarzschildLike[Expr_]:=Module[{SchwarzschildLikeExpr=Expr},

	(*-----------------------------------------------------*)
	(*  Even inside scalars, impose the coordinate ansatz  *)
	(*-----------------------------------------------------*)

	SchwarzschildLikeExpr=SchwarzschildLikeExpr/.{xAct`xTensor`Scalar->RawSchwarzschildLike};

	(*---------------------------------------*)
	(*  Then impose the ansatz on the whole  *)
	(*---------------------------------------*)

	SchwarzschildLikeExpr//=RawSchwarzschildLike;	

	(*------------------------------------------------------------------*)
	(*  Assume we evaluate at a point in the chart with nonzero radius  *)
	(*------------------------------------------------------------------*)

	SchwarzschildLikeExpr//=Simplify;	

	SchwarzschildLikeExpr];

How to set up reduced radial-function components of a tensor field which is not the metric, of course in MoND we have the unit-timelike vector field. To implement this we try: 

Comment@"We wish to define a unit-timelike one-form.";

DefTensor[A[-a],M4,PrintAs->"\[ScriptCapitalA]"];

Expr=A[{-a,-SphericalPolar}];
DisplayExpression@Expr;
Expr//=ComponentArray;
Expr//=ToValues;
DisplayExpression@Expr;

Comment@"We know that this one-form has the property of being unit-timelike, and that the Killing algebra is spherical. So, we define a couple of scalar functions.";

DefScalarFunction[A1,PrintAs->"\[CapitalPhi]"];
DefScalarFunction[A2,PrintAs->"\[CapitalPsi]"];

AllComponentValues[A[{-a,-SphericalPolar}],{A1[cr[]],B2[cr[]]*Sqrt[A1[cr[]]^2/B1[cr[]]^2-1],0,0}];

Expr=A[{-a,-SphericalPolar}];
DisplayExpression@Expr;
Expr//=ComponentArray;
DisplayExpression@Expr;
Expr//=ToValues;
DisplayExpression@Expr;

To check that a simple expression is carried properly to the component form: 

Expr=CD[-a]@Phi[]*CD[-b]@Psi[]*G[a,b];
DisplayExpression@Expr;
Expr//=ToSchwarzschildLike;
DisplayExpression@Expr;

Next something more advanced, we want to show that our one-form really does the job: 

Expr=A[-a]*A[a];
DisplayExpression@Expr;
Expr//=SeparateMetric[G];
Expr//=ScreenDollarIndices;
DisplayExpression@Expr;
Expr//=ToSchwarzschildLike;
DisplayExpression@Expr;

Great. Now let's check that this can be used for more complex expressions: 

Expr=A[-a]*A[-b]*RicciCD[a,b];
DisplayExpression@Expr;
Expr//=SeparateMetric[G];
Expr//=ScreenDollarIndices;
DisplayExpression@Expr;
Expr//=ToSchwarzschildLike;
DisplayExpression@Expr;

Now know already how to obtain field equations from basically any tensor field theory with abstract Penrose slot indices, but you need to be able to get the components of those equations. You can typically adapt the following steps: 

Expr=G[-a,-b];
DisplayExpression@Expr;
Expr=ToSchwarzschildLike/@(Expr//ToBasis[SphericalPolar]//ComponentArray);
DisplayExpression@Expr;

Going to conferences Top

It is very important that you attend lots of conferences during your Ph.D.. Conferences are an opportunity for you to do several things;

  1. Expose yourself to new ideas in your field. Stagnation is death.
  2. Develop your networking skills, and attract collaborators.
  3. Develop your public speaking skills.
  4. Foster interest in your research.
  5. Expose yourself, your research and your research group to expert criticism.
  6. Seek employment opportunities if you plan to stay in academia.
  7. Travel the world, and leave not a cent of grant money unspent!
Some conferences have sign-up fees, most engender travel expenses. You usually need to register in advance, and submit an abstract for selection if you plan to give a talk. Eventually (when you are rich and famous) the chemical potential reverses and you will be invited as a speaker. Availability of funds for conferences will vary according to your studentship.

There are a few conferences on the horizon;

  1. Rencontres de Moriond, 18th-25th March 2023. Moriond is a recurring conference divided into blocks (18-25/03 : Electroweak Interactions & Unified Theories 18-25/03 : Gravitation 25/03-01/04 : Mesoscopic Physics 25/03-01/04 : QCD and High Energy Interactions). The application deadline has passed (31st January) but there may still be space.
  2. I've heard a rumour of something in-the-works to be organised by Jose Beltrán Jiménez in Salamanca. Watch this space, and I'll update...
  3. There will be a conference "complex" taking place in the summer of 2023, as organised by the Corfu Summer Institute.
  4. The 32nd Texas Symposium on Relativistic Astrophysics is supposed to be held in Shanghai, but as far as I can tell it does not yet have a website. Last year it was in Prague.

Prospective Ph.D. Students Top

This fall (2022) I will be advertising a Ph.D. position, to be jointly supervised with other group members. Research themes will include gravitational theory, quantum gravity and modified gravity. The advert to appear on the Cavendish Astrophysics Ph.D. topics page will run as follows:

W Barker, M Hobson & A Lasenby: Gravitational theory and quantum gravity.

  1. Fundamental theory of the gravitational interaction: gauge-theoretic and geometric formulations (torsion, non-metricity); canonically-driven methods; theoretical constraints on less conservative formulations (e.g. relativistic MoND, gravity as an order parameter of the fermion vacuum).
  2. Perturbative quantum gravity: particle spectra in strong backgrounds; effective field theory of gravity.
  3. Non-perturbative quantum gravity: lattice regularisations including dynamical triangulations; novel applications of geometric algebra.
  4. Phenomenology of modified gravity: classical dynamics and exact solutions; cosmological perturbation theory; primordial non-Gaussianity and shape templates; parametersised post-Newtonian formalism; detection of non-Riemannian geometries; implications for fermion physics. Links with cosmological inference, numerics and computation in W Handley's group.
  5. Computer algebra: use of high-performance computing to solve symbolic (non-numerical) problems in gravity theory; surveying the theory-space for viable Lagrangia; theory-agnostic tools (HiGGS, PSALTer).

In general, these topics need not be binding or exhaustive if our research interests align on some other project. These matters could be discussed at the informal "interview" or via email.

For most applicants... Top

The main bottleneck for obtaining a PhD in the UK is securing funding, which for international applicants is especially competitive as there are not many funds which can cover the higher University fees. If there are any independent funding bodies from your home country or otherwise from which you can secure support to fund or partially fund your degree, then this will substantially improve your chances of finding a PhD place in the UK. There are also language requirements for international students, for which Cambridge is higher than usual (unfairly in my view).

For most applicants (home and international), the deadline for securing funding from the University itself will dictate the application deadline, and this will be midnight on the 1st December, 2022. I'd strongly recommend you submit all components of the application at least 24 hours in advance, due to potential ambiguities over the cutoff.

The rest of this information is based on the Cavendish Astrophysics Group Graduate Research Opportunities for October 2023 entry page, which links to a description of the admissions procedure.

You must apply through the University-wide Board of Graduate Study (BoGS). A good place to start is from the advice on postgraduate application deadlines. From there you can establish your funding deadlines from the information page on how to find funding. The most relevant funding sources are consolidated into something called the Cambridge Trust: the Trust deadline is what establishes the 1st December deadline above. The Trust allows you to search for available scholarships. Particularly relevant to overseas applicants is the Gates Scholarship. Gates has a rather extensive application process. There may well be other (departmental or college-specific) funding sources that are not part of the Trust. For UK applicants, note that the BoGS application procedure causes you to be considered for STFC funding (i.e. UK government funding).

You must also apply directly to our research group (departmental application), and for this there is a dedicated application form. You should do this by the same application deadline as above, December 1st. Unhelpfully, I learned last week that the form is out of date since last year, and neither Professor Hobson's name nor my own are listed where it says "Please select the name/s of the main contact person/supervisor you would be interested in working with". For the time being, you should select "Will Handley", and make it clear that you are applying to the Barker/Hobson/Lasenby abstract in one of the three funding information boxes at the end of the form, and also email the administrator at admissions@mrao.cam.ac.uk. We will then redirect applications at our end.

Once the applications are submitted, informal "interviews" will follow.

For a small minority... Top

For those of you who have some external source of funding available (not associated with the University, Cambridge Trust, etc.), you will notice that many of the links above mention later deadlines, extending even into the new year. I would still encourage you to register interest and apply by the 1st December deadline.