I am the creator and maintainer of multiple software packages for use in theoretical physics. I work mostly in the Wolfram Language, but also in Maple, Julia, Python and C++.

All my software is dual-hosted on GitHub and GitLab.

View GitHub Profile View GitLab Group

Below are my main projects with live repository information pulled from GitHub.

license arXiv arXiv arXiv arXiv arXiv arXiv arXiv arXiv

PSALTer: Particle Spectrum for Any Tensor Lagrangian

Version 2.0.1

  • Removed RectanglePacking from package dependencies.
  • Updated README.md.

License

Copyright Β© 2022 Will Barker, Giorgos Karananas, Carlo Marzo, Claire Rigouzzo and Haochen Tu.

PSALTer is distributed as free software under the GNU General Public License (GPL).

PSALTer is provided without warranty, or the implied warranty of merchantibility or fitness for a particular purpose.

If PSALTer was useful to your research, please cite us using the following BibTeX:

@article{Barker:2024juc,
    author = "Barker, Will and Marzo, Carlo and Rigouzzo, Claire",
    title = "{PSALTer: Particle Spectrum for Any Tensor Lagrangian}",
    eprint = "2406.09500",
    archivePrefix = "arXiv",
    primaryClass = "hep-th",
    month = "6",
    year = "2024"
}
@article{Barker:2025qmw,
    author = "Barker, Will and Karananas, Georgios K. and Tu, Haochen",
    title = "{The particle spectra of parity-violating theories: A less radical approach and an upgrade of PSALTer}",
    eprint = "2506.02111",
    archivePrefix = "arXiv",
    primaryClass = "hep-th",
    month = "6",
    year = "2025"
}

About

PSALTer is a software package for Wolfram (formerly Mathematica) designed to predict the propagating quantum particle states in any tensorial field theory, including (but not limited to) just about any theory of gravity. The free action $S_{\text{F}}$ must have the structure

S_{\text{F}}=\int\mathrm{d}^4x\ \zeta(x)^{\text{T}}\cdot\Big[\mathcal{O}(\partial)\cdot\zeta(x)-j(x)\Big],

where the ingredients are:

  • The dynamical fields $\zeta(x)$ are real tensors, which may be a collection of distinct fields, each field having some collection of spacetime indices ($\mu$, $\nu$, etc.), perhaps with some symmetry among the indices.
  • The wave operator $\mathcal{O}(\partial)$ is a real, second-order differential operator constructed from the flat-space metric $\eta_{\mu\nu}$, partial derivative $\partial_\mu$ and totally antisymmetric $\epsilon^{\mu\nu\sigma\lambda}$ tensor, linearly parameterised by a collection of coupling coefficients. Note that Ostrogradsky’s theorem discourages higher-derivative operators, but even if it did not we note that the apparent order may always be lowered by the introduction of extra fields.
  • The source currents $j(x)$ are conjugate to the fields $\zeta(x)$. They encode all external interactions to second order in fields, whilst keeping the external dynamics completely anonymous.

Example: massive gravity

As a demonstration, we consider the Fierz-Pauli linearised massive gravity theory

S=\int\mathrm{d}^4x\ \Big[\alpha\big(-\partial^\mu h_{\mu\nu}\partial^\nu h+\tfrac{1}{2}\partial_\mu h\partial^\mu h-\tfrac{1}{2}\partial_\sigma h^{\mu\nu}\partial_\sigma h_{\mu\nu}+\partial_\nu h^{\mu\nu}\partial^\sigma h_{\mu\sigma}\big)+\beta\big(h^{\mu\nu}h_{\mu\nu}-h^2\big)+h^{\mu\nu}T_{\mu\nu}\Big],

where $\alpha$ and $\beta$ are coupling coefficients, $h_{\mu\nu}$ is the metric perturbation with trace $h\equiv h_{\mu}^{\mu}$, and $T^{\mu\nu}$ is the linearised stress-energy tensor of matter, which is the source conjugate to $h_{\mu\nu}$.

In a fresh notebook we first load the package:

<<xAct`PSALTer`;

Next, we define Lagrangian couplings $\alpha$ and $\beta$ as Coupling1 and Coupling2 using the command DefConstantSymbol from xAct:

DefConstantSymbol[Coupling1,PrintAs->"\[Alpha]"];
DefConstantSymbol[Coupling2,PrintAs->"\[Beta]"];

Next, we use the command DefField from PSALTer to define the metric perturbation $h_{\mu\nu}$ as the symmetric, rank-two tensor field MetricPerturbation:

DefField[
    MetricPerturbation[-a,-b],
    Symmetric[{-a,-b}],
    PrintAs->"\[ScriptH]",
    PrintSourceAs->"\[ScriptCapitalT]"
];

The output should look like:

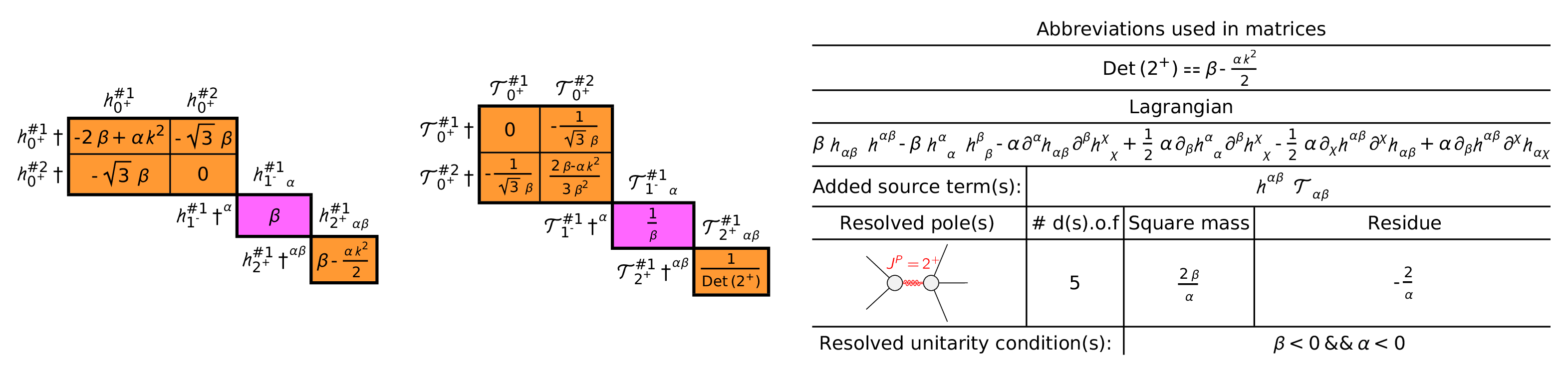
To compute the spectrum, we plug the Lagrangian into the ParticleSpectrum function from PSALTer:

ParticleSpectrum[
    Coupling1*(
	(1/2)*CD[-b]@MetricPerturbation[a,-a]*CD[b]@MetricPerturbation[c,-c]
	-CD[a]@MetricPerturbation[-a,-b]*CD[b]@MetricPerturbation[c,-c]
	-(1/2)*CD[-c]@MetricPerturbation[a,b]*CD[c]@MetricPerturbation[-a,-b]
	+CD[-b]@MetricPerturbation[a,b]*CD[c]@MetricPerturbation[-a,-c]
    )
    +Coupling2*(
        MetricPerturbation[-a,-b]*MetricPerturbation[a,b]
        -MetricPerturbation[a,-a]*MetricPerturbation[b,-b]
    ),
    TheoryName->"MassiveGravity",	
    MaxLaurentDepth->3
];

The output should look like:

Documentation

The package includes a notebook with the basic example above. This notebook will try to save PDF graphics files to the directory in which it is saved, so it is better not to run it from within your actual installation. For instance, to copy the file to your home directory and run it there using the front end (notebook), you can use: ```console, bash [user@system PSALTer]$ cp xAct/PSALTer/Documentation/English/Examples.nb ~/Examples.nb [user@system PSALTer]$ cd [user@system English]$ wolframnb Examples.nb &

The theory underlying the package is developed across two papers:
- [The first paper](https://arxiv.org/abs/2406.09500) presents _PSALTer_ v 1.0.0 (basic functionality).
- [The second paper](https://arxiv.org/abs/2503.#####) presents _PSALTer_ v 2.0.0 (extension to parity violation and breaking changes).

## General use 

### Pre-defined geometry

When you first run `` <<xAct`PSALTer` `` the software defines a Minkowski manifold with the ingredients:

| _Wolfram Language_      | Output format                            | Meaning                      |
|-------------------------|------------------------------------------|------------------------------|
| `a`, `b`, `c`, ..., `z` | $\alpha$, $\beta$, $\gamma$, ... $\zeta$ | Cartesian coordinate indices |
| `G[-m,-n]`              | $\eta_{\mu\nu}$                          | Minkowski metric             |
| `CD[-m]@`               | $\partial_{\mu}$                         | Partial derivative           |
| `epsilonG[-m,-n,-s,-l]` | $\epsilon_{\mu\nu\sigma\lambda}$         | Totally antisymmetric tensor |

For those familiar with _xAct_, note that calls to `DefManifold` and `DefMetric` are made internally at this stage. The minimal workflow in _PSALTer_ is to compute spectra based on a free Lagrangian density which has already been worked out, and simply needs to be plugged into the `ParticleSpectrum` function once the relevant fields are defined using `DefField` and the relevant coupling constants are defined using `DefConstantSymbol`. A more advanced workflow uses the geometric environment of _PSALTer_ and various tools from _xAct_ to first compute the free Lagrangian density by _linearising_ some other model. In the latter case, it is important to first understand more about the geometric environment of _PSALTer_, which is established internally by the following calls:
```mathematica
DefManifold[M4,4,IndexRange[{a,z}]];
DefMetric[-1,G[-a,-c],CD,{",","\[PartialD]"},PrintAs->"\[Eta]",FlatMetric->True,SymCovDQ->True];

In particular, the flat metric environment can be inconvenient when the model to be linearised is gravitational in nature, relying on some curvature tensor. At the practical level, one can always obtain the correct linearisation by reinterpreting the model as a field theory on flat spacetime: this approach is guaranteed to work because particle physics is not actually sensitive to geometry per se. Alternatively, one can prepare the linearised expression in a separate xAct session, taking advantage of the full geometric interpretation, and then copy the resulting Wolfram Language expression directly into the PSALTer session. Care must be taken in this case to ensure that the indices are correctly matched.

Function DefField

DefField[<Fld>[]]

defines a scalar field <Fld> and exports the field kinematics to a PDF file.

DefField[<Fld>[<Ind1>,<Ind2>,...]]

defines a tensor field <Fld> with indices <Ind1>, <Ind2>, etc., and exports the field kinematics to a PDF file.

DefField[<Fld>[<Ind1>,<Ind2>,...],<Symm>]

defines a tensor field <Fld> with indices <Ind1>, <Ind2>, etc. and symmetry <Symm>, and exports the field kinematics to a PDF file.

Details and options

  • The syntax of DefField is almost identical to that of DefTensor in xTensor.
  • Up to three comma-separated indices may be drawn from the contravariant a, b, c, up to z, the covariant -a, -b, -c, up to -z, or any admixture.
  • It is strongly recommended to use clear, alphanumeric names for <Fld>, because the name of the field kinematics file will be FieldKinematics<Fld>.pdf. As explained below, the PrintAs option allows the user to specify the symbol used for formatting the field in the front end (notebook) and the exported PDFs.
  • The symmetry <Symm> can be one of the following, where <SymmInd1>, <SymmInd2>, etc. are any two or three fully covariant or contravariant, comma-separated indices drawn verbatim from <Ind1>, <Ind2>, etc.:
    • Symmetric[{<SymmInd1>,<SymInd2>,...}] denotes symmetrized indices.
    • Antisymmetric[{<SymmInd1>,<SymInd2>,...}] denotes antisymmetrized indices.
  • In the front end (notebook) the currently-evaluating subroutine is displayed temporarily.
  • In the terminal, the currently-evaluating subroutine is sent to STDOUT.
  • Whilst DefField prints a preview of the field kinematics in the front end (notebook) it always returns Null.
  • The following options may be given:
    • PrintAs is the symbol that <Fld> will use for formatting. In the front end (notebook), symbols can be entered directly. Programmatically, the Wolfram Language admits named characters such as "\[<Name>]". The default is $\zeta$ or "\[Zeta]".
    • PrintSourceAs is the symbol that the source conjugate to <Fld> will use for formatting. The syntax is identical to PrintAs. The default is $j$ or "\[ScriptJ]".

Function ParticleSpectrum

ParticleSpectrum[<Lagr>];

computes the spectrum of the Lagrangian <Lagr>, and exports a spectrograph to a PDF file.

Details and options

  • The Lagrangian <Lagr> must be a valid, linearised Lagrangian density. The expression must be a Lorentz-scalar. Each term must be quadratic in field(s) which have already been defined using DefField. Each term must be linear in coupling constant(s) which have already been defined using DefConstantSymbol from xTensor. Other allowed ingredients are CD, G and epsilonG. Do not try to include the term coupling the fields to their conjugate sources: this is accounted for internally.
  • In the front end (notebook) the currently-evaluating subroutine is displayed temporarily.
  • In the terminal, the currently-evaluating subroutine is sent to STDOUT.
  • Whilst ParticleSpectrum prints a preview of the spectrograph in the front end (notebook) it always returns Null.
  • The following options may be given:
    • TheoryName is a mandatory option and must be set to an alphanumeric string "<ThrNme>". The name of the spectrograph file will be ParticleSpectrograph<ThrNme>.pdf.
    • Neglect must be a list of the form &#123;&#123;<Spn1>,<Pty1>&#125;,&#123;<Spn2>,<Pty2>&#125;,...&#125;, enumerating the spins and parities of the sectors which are to be neglected in the analysis, where <Spn1> and <Spn2> etc. are 0, 1, 2 or 3 and <Pty1>, <Pty2> etc. are 1 or -1. The massless spectrum will not be computed if any sectors have been neglected. The default is &#123;&#125;.
    • MasslessSpectrum can be True or False. If False, the massless spectrum is not computed. The default is True.
    • MaxLaurentDepth can be 1, 2 or 3. This sets the maximum positive integer $n$ for which the $1/k^{2n}$ pole residues at $k=0$ are requested. The default is 1 (quadratic), from which the massless spectrum can be obtained. Setting higher $n$ naturally leads to longer wallclock times, but also allows any pathological higher-order (quartic and hexic) poles to be identified, down to the requested depth.
    • ShowPropagator can be True or False. If True, the propagator is displayed. The default is False.
    • AspectRatio can be Landscape or Portrait. This sets the aspect ratio of the spectrograph. The default is Landscape.

Quickstart

Requirements

Basic hardware requirements

  • A multi-core processor (recommended, note that most modern PCs are multi-core).
  • An internet connection (recommended for PSALTer to interrogate the Wolfram Function Repository).

Operating systems

Software dependencies

Installation

:warning: Note that Mathematica was re-branded as Wolfram on July 31 2024 with the release of Wolfram v 14.1. You may still be able to install PSALTer in older versions of Wolfram (formerly Mathematica) by replacing Wolfram with Mathematica in the various paths below.

Linux

  1. Prepare. Make sure your system satisfies all the requirements.
  2. Download. You can download the latest release from the panel on the right, and unzip using: ```console, bash [user@system ~]$ unzip ~/Downloads/PSALTer* [user@system ~]$ mv ~/PSALTer* ~/PSALTer 
    Alternatively, if you have _git_ installed, the following _bash_ command will download _PSALTer_ into the home directory:
```console, bash, git
[user@system ~]$ git clone https://github.com/wevbarker/PSALTer
  3. Install. To perform the installation, the sources need only be copied to the location of the other xAct sources. For a global installation of xAct this may require: ```console, bash [user@system ~]$ cd PSALTer/xAct [user@system xAct]$ sudo cp -r PSALTer /usr/share/Wolfram/Applications/xAct/ 
    For a local installation of _xAct_, the path may be vary:
```console, bash
[user@system xAct]$ cp -r PSALTer ~/.Wolfram/Applications/xAct/

macOS

:warning: Note that macOS is not recommended for use with PSALTer.

  1. Prepare. Make sure your system satisfies all the requirements.
  2. Download. You can download the latest release from the panel on the right, and unzip using: ```console, zsh user@system ~ % unzip ~/Downloads/PSALTer* user@system ~ % mv ~/PSALTer* ~/PSALTer 
    Alternatively, if you have _git_ installed, the following _zsh_ command will download _PSALTer_ into the home directory:
```console, zsh, git
user@system ~ % git clone https://github.com/wevbarker/PSALTer
  3. Install. To perform the installation, the sources need only be copied to the location of the other xAct sources. For a global installation of xAct this may require: ```console, zsh user@system ~ % cd PSALTer/xAct user@system xAct % sudo cp -r PSALTer /Library/Mathematica/Applications/xAct/ 
    For a local installation of _xAct_, the path may be vary:
```console, zsh 
user@system xAct % cp -r PSALTer ~/Library/Mathematica/Applications/xAct/
  4. Make sure you’ve read the known bugs that can affect macOS users.

Microsoft Windows

:warning: Note that Microsoft Windows is not recommended for use with PSALTer.

  1. Prepare. Make sure your system satisfies all the requirements.
  2. Download. You can download the latest release from the panel on the right, and unzip in File Explorer using right-click and Extract All. Alternatively, if you have git installed, the following cmd command will download PSALTer into the home directory: console, cmd, git C:\Users\user> git clone https://github.com/wevbarker/PSALTer
  3. Install. To perform the installation, the sources need only be copied to the location of the other xAct sources. For a global installation of xAct, you may need to open File Explorer using right-click and Run as administrator. Alternatively, use the following cmd commands (again, opening cmd using Run as administrator): ```console, cmd C:\Users\user> cd PSALTer C:\Users\user\PSALTer> xcopy /e /k /h /i xAct\ β€œC:\Program Files\Wolfram Research\Mathematica\14.0\AddOns\Applications\xAct" 
    For a local installation of _xAct_, the path may be vary:
```console, cmd 
C:\Users\user\PSALTer> xcopy /e /k /h /i xAct\ "C:\Users\user\AppData\Roaming\Mathematica\Applications\xAct\"
  4. Make sure you’ve read the known bugs that can affect Microsoft Windows users.

Getting help

There are several ways to get help:

  • The xAct google group contains a well established, highly active and very friendly community of researchers. Feel free to start a New conversation by posting a minimal working example of your code.
  • For private correspondence, you can email us at barker@fzu.cz.
  • Alternatively you may wish to raise a New issue on GitHub.

Known bugs

  1. A sporadic error where some of the gauge symmetries are not identified. The algorithm uses numerical methods to obtain the gauge symmetries, which involve random number generation at runtime. The error can usually be fixed by re-running ParticleSpectrum.
  2. A sporadic error on Linux and macOS involving missing or incorrect glyphs in the output graphic. On Linux, the problem has to do with installed fonts, and it may be solved by upgrading your system (and rebooting).

Acknowledgements

PSALTer was improved by many useful discussions with Jaakko Annala, Stephanie Buttigieg, DraΕΎen Glavan, Will Handley, Mike Hobson, Manuel Hohmann, Damianos Iosifidis, Georgios Karananas, Anthony Lasenby, Yun-Cherng Lin, Oleg Melichev, Yusuke Mikura, Vijay Nenmeli, Roberto Percacci, Syksy RΓ€sΓ€nen, Cillian Rew, Ignacy Sawicki, Zhiyuan Wei, David Yallup, Haoyang Ye, and Sebastian Zell.

This work used the DiRAC Data Intensive service (CSD3 www.csd3.cam.ac.uk) at the University of Cambridge, managed by the University of Cambridge University Information Services on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). The DiRAC component of CSD3 at Cambridge was funded by BEIS, UKRI and STFC capital funding and STFC operations grants. DiRAC is part of the UKRI Digital Research Infrastructure.

This work also used the Newton compute server, access to which was provisioned by Will Handley using an ERC grant.

WB is grateful for the kind hospitality of Leiden University and the Lorentz Institute, and the support of Girton College, Cambridge, Marie SkΕ‚odowska-Curie Actions and the Institute of Physics of the Czech Academy of Sciences. The work of CM was supported by the Estonian Research Council grants PRG1677, RVTT3, RVTT7, and the CoE program TK202 β€œFundamental Universe”. CR acknowledges support from a Science and Technology Facilities Council (STFC) Doctoral Training Grant.

Co-funded by the European Union (Physics for Future – Grant Agreement No. 101081515). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or European Research Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.

Last commit:
Thursday, 5 June 2025Latest release:
v2.0.1

View full repository on GitHub β†’
View full repository on GitLab β†’

license Mathematica xAct

Hamilcar: MCP-compliant tools for Hamiltonian analysis

Version 0.0.0-developer

  • Initial development version of the canonical field theory package.
  • Extends xAct for time-dependent field calculations.

License

Copyright Β© 2023 Will E. V. Barker

Hamilcar is distributed as free software under the GNU General Public License (GPL).

Hamilcar is provided without warranty, or the implied warranty of merchantibility or fitness for a particular purpose.

If Hamilcar was useful to your research, please cite us using the following BibTeX:

@misc{Barker:2025Hamilcar,
    author = "Barker, Will E. V.",
    title = "{Hamilcar: A Mathematica Package for Canonical Field Theory}",
    year = "2025",
    note = "In development"
}

About

Hamilcar is a software package for Wolfram (formerly Mathematica) designed to provide robust tools for agentic systems to perform Hamiltonian analysis in canonical field theory. The overall goal is to enable AI agents and automated systems to conduct sophisticated field theory calculations through well-defined interfaces.

The package focuses on canonical field theory calculations in 3+1 dimensions, where the action $S$ has the structure

S=\int\mathrm{d}t\int\mathrm{d}^3x\ \Big[\pi_\psi(x,t)\cdot\dot{\psi}(x,t)-H(\psi,\pi_\psi)\Big],

where the ingredients are:

  • The dynamical fields $\psi(x,t)$ are real tensors on the spatial manifold, which may be a collection of distinct fields, each field having some collection of spatial indices ($a$, $b$, etc.), perhaps with some symmetry among the indices.
  • The conjugate momenta $\pi_\psi(x,t)$ are the canonical momenta conjugate to the fields $\psi(x,t)$.
  • The Hamiltonian density $H(\psi,\pi_\psi)$ is constructed from the fields, momenta, spatial metric, and spatial derivatives.

Example: scalar field theory

As a demonstration, we consider a simple scalar field theory in 3+1 dimensions

S=\int\mathrm{d}^4x\ \Big[-\tfrac{1}{2}\partial^\mu\phi\partial_\mu\phi+\tfrac{1}{2}m^2\phi^2\Big],

where $m$ is the mass parameter.

In a fresh notebook we first load the package:

<<xAct`Hamilcar`;

Next, we define a scalar field using the command DefCanonicalField:

DefCanonicalField[Phi[],FieldSymbol->"\[Phi]",MomentumSymbol->"\[Pi]"];

We can then compute Poisson brackets between quantities:

PoissonBracket[Phi[],ConjugateMomentumPhi[]];

Documentation

Comprehensive documentation with worked examples is available as an interactive Mathematica notebook at xAct/Hamilcar/Documentation/English/Documentation.nb. This documentation includes:

  • General Relativity: Complete walkthrough of the ADM formalism, including constraint definitions, smearing functions, and computation of the Dirac hypersurface deformation algebra
  • Maxwell Theory: Canonical electromagnetic field theory demonstrating Gauss constraint analysis and the Dirac algorithm

To access the documentation, open the notebook file in Mathematica:

NotebookOpen["xAct/Hamilcar/Documentation/English/Documentation.nb"]

This provides an interactive notebook with all calculations, explanations, and mathematical results ready to execute.

Agentic Integration

While Hamilcar currently provides a comprehensive Mathematica interface for canonical field theory calculations, the ultimate goal is to enable seamless integration with agentic systems. The requisite JSON-RPC interface that will allow AI agents to programmatically access Hamilcar’s functionality is yet to be developed.

This future interface will enable:

  • Automated constraint algebra analysis
  • Programmatic field theory calculations
  • Integration with larger agentic workflows
  • Standardized communication protocols for field theory operations

General use

Pre-defined geometry

When you first run <<xAct`Hamilcar` the software defines a three-dimensional spatial hypersurface with the ingredients:

Wolfram Language Output format Meaning
a, b, c, …, z $a$, $b$, $c$, … $z$ Spatial coordinate indices (corresponding to adapted coordinates in the ADM prescription)
G[-a,-b] $h_{ab}$ Induced metric on the spatial hypersurface
CD[-a]@ $\nabla_{a}$ Spatial covariant derivative
epsilonG[-a,-b,-c] $\epsilon_{abc}$ Induced totally antisymmetric tensor on the spatial hypersurface

For those familiar with xAct, note that calls to DefManifold and DefMetric are made internally at this stage. The package establishes a spatial manifold M3, creating the necessary geometric structure for canonical field theory calculations.

Function DefCanonicalField

DefCanonicalField[<Fld>[]]

defines a scalar canonical field <Fld> and its conjugate momentum ConjugateMomentum<Fld>.

DefCanonicalField[<Fld>[<Ind1>,<Ind2>,...]]

defines a tensor canonical field <Fld> and its conjugate momentum ConjugateMomentum<Fld> with indices <Ind1>, <Ind2>, etc..

DefCanonicalField[<Fld>[<Ind1>,<Ind2>,...],<Symm>]

defines a tensor canonical field <Fld> and its conjugate momentum ConjugateMomentum<Fld> with indices <Ind1>, <Ind2>, etc. and symmetry <Symm>.

Details and options

  • The syntax of DefCanonicalField follows similar patterns to DefTensor in xTensor.
  • Any number of comma-separated indices may be drawn from the contravariant a, b, c, up to z, the covariant -a, -b, -c, up to -z, or any admixture.
  • The symmetry <Symm> can be one of the following (or any admixture allowed by DefTensor):
    • Symmetric[{<SymmInd1>,<SymInd2>,...}] denotes symmetrized indices.
    • Antisymmetric[{<SymmInd1>,<SymInd2>,...}] denotes antisymmetrized indices.
  • If the global variable $DynamicalMetric is set to True, then:
    • The spatial metric G is automatically registered as a canonical field, and ConjugateMomentumG is defined.
    • All conjugate momenta are automatically defined as tensor densities of weight one (the effects of this are only seen by the G-variations performed internally by PoissonBracket).
  • The following options may be given:
    • FieldSymbol is the symbol that <Fld> will use for display formatting.
    • MomentumSymbol is the symbol that the conjugate momentum will use for display formatting.

Function PoissonBracket

PoissonBracket[<Op1>,<Op2>]

computes the Poisson bracket between operators <Op1> and <Op2>.

Details and options

  • The operators <Op1> and <Op2> must be expressions involving:
    • Canonical fields and their conjugate momenta which have been defined using DefCanonicalField.
    • Tensors which have been defined on the manifold M3 using DefTensor, and which are assumed always to be independent of the canonical fields.
    • Derivatives via CD of canonical and non-canonical quantities, the spatial metric G, and the totally antisymmtric tensor epsilonG.
    • Constant symbols which have been defined using DefConstantSymbol (or DefNiceConstantSymbol from the xTras package).
  • The function automatically generates smearing tensors unless $ManualSmearing is set to True.
  • When $DynamicalMetric is set to True, the G-sector contributions are included.
  • The function computes variational derivatives with respect to all registered fields and momenta.

Function TotalFrom

TotalFrom[<Expr>]

expands composite expressions to canonical variable form by applying all registered expansion rules.

Details and options

  • The function converts composite quantities (like constraint expressions, traces, or field combinations) into explicit expressions involving only the fundamental canonical variables: fields, conjugate momenta, and their spatial derivatives.
  • This expansion is essential before computing Poisson brackets, as bracket calculations require expressions to be written in terms of the canonical variables registered by DefCanonicalField.
  • The function applies all rules stored in the internal list $FromRulesTotal, which are populated using PrependTotalFrom.

Function TotalTo

TotalTo[<Expr>]

converts expressions from canonical variable form back to compact notation using registered contraction rules.

Details and options

  • The function performs the inverse operation of TotalFrom, converting expressions written in terms of canonical variables back to more compact composite notation.
  • This is primarily used for presentation purposes to make final results more readable.
  • The function applies all rules stored in the internal list $ToRulesTotal, which are populated using PrependTotalTo.
  • Unlike TotalFrom, this function is optional in most calculations.

Function PrependTotalFrom

PrependTotalFrom[<Rule>]

registers an expansion rule to convert a composite quantity to canonical variable form.

Details and options

  • The function adds <Rule> to the front of the internal list $FromRulesTotal used by TotalFrom.
  • Typically used with MakeRule expressions that define composite quantities in terms of canonical variables.
  • Essential for setting up the expansion system before performing Poisson bracket calculations.
  • Example usage: FromSuperHamiltonian//PrependTotalFrom registers the rule to expand the super-Hamiltonian constraint.

Function PrependTotalTo

PrependTotalTo[<Rule>]

registers a contraction rule to convert canonical variable expressions back to compact notation.

Details and options

  • The function adds <Rule> to the front of the internal list $ToRulesTotal used by TotalTo.
  • Used with rules that convert expanded canonical expressions back to composite quantities.
  • Provides the symmetric counterpart to PrependTotalFrom for bidirectional transformations.
  • Less commonly used than PrependTotalFrom as conversion back to compact form is often optional.

Function FindAlgebra

This function is undocumented and under active development. The purpose of the function is to determine constraint algebroids.

Function TimeD

This function is undocumented and under active development. The purpose of the function is to manage time derivatives of fields.

Quickstart

Requirements

Basic hardware requirements

  • A multi-core processor (recommended, note that most modern PCs are multi-core).
  • An internet connection (recommended for Hamilcar to interrogate the Wolfram Function Repository).

Operating systems

Software dependencies

Installation

:warning: Note that Mathematica was re-branded as Wolfram on July 31 2024 with the release of Wolfram v 14.1. You may still be able to install Hamilcar in older versions of Wolfram (formerly Mathematica) by replacing Wolfram with Mathematica in the various paths below.

Linux

  1. Prepare. Make sure your system satisfies all the requirements.
  2. Download. You can download the latest release from the panel on the right, and unzip using: ```console, bash [user@system ~]$ unzip ~/Downloads/Hamilcar* [user@system ~]$ mv ~/Hamilcar* ~/Hamilcar 
    Alternatively, if you have _git_ installed, the following _bash_ command will download _Hamilcar_ into the home directory:
```console, bash, git
[user@system ~]$ git clone https://github.com/wevbarker/Hamilcar
  3. Install. To perform the installation, the sources need only be copied to the location of the other xAct sources. For a global installation of xAct this may require: ```console, bash [user@system ~]$ cd Hamilcar/xAct [user@system xAct]$ sudo cp -r Hamilcar /usr/share/Wolfram/Applications/xAct/ 
    For a local installation of _xAct_, the path may be vary:
```console, bash
[user@system xAct]$ cp -r Hamilcar ~/.Wolfram/Applications/xAct/

macOS

:warning: Note that macOS is not recommended for use with Hamilcar.

  1. Prepare. Make sure your system satisfies all the requirements.
  2. Download. You can download the latest release from the panel on the right, and unzip using: ```console, zsh user@system ~ % unzip ~/Downloads/Hamilcar* user@system ~ % mv ~/Hamilcar* ~/Hamilcar 
    Alternatively, if you have _git_ installed, the following _zsh_ command will download _Hamilcar_ into the home directory:
```console, zsh, git
user@system ~ % git clone https://github.com/wevbarker/Hamilcar
  3. Install. To perform the installation, the sources need only be copied to the location of the other xAct sources. For a global installation of xAct this may require: ```console, zsh user@system ~ % cd Hamilcar/xAct user@system xAct % sudo cp -r Hamilcar /Library/Mathematica/Applications/xAct/ 
    For a local installation of _xAct_, the path may be vary:
```console, zsh 
user@system xAct % cp -r Hamilcar ~/Library/Mathematica/Applications/xAct/

Microsoft Windows

:warning: Note that Microsoft Windows is not recommended for use with Hamilcar.

  1. Prepare. Make sure your system satisfies all the requirements.
  2. Download. You can download the latest release from the panel on the right, and unzip in File Explorer using right-click and Extract All. Alternatively, if you have git installed, the following cmd command will download Hamilcar into the home directory: console, cmd, git C:\Users\user> git clone https://github.com/wevbarker/Hamilcar
  3. Install. To perform the installation, the sources need only be copied to the location of the other xAct sources. For a global installation of xAct, you may need to open File Explorer using right-click and Run as administrator. Alternatively, use the following cmd commands (again, opening cmd using Run as administrator): ```console, cmd C:\Users\user> cd Hamilcar C:\Users\user\Hamilcar> xcopy /e /k /h /i xAct\ β€œC:\Program Files\Wolfram Research\Mathematica\14.0\AddOns\Applications\xAct" 
    For a local installation of _xAct_, the path may be vary:
```console, cmd 
C:\Users\user\Hamilcar> xcopy /e /k /h /i xAct\ "C:\Users\user\AppData\Roaming\Mathematica\Applications\xAct\"

Getting help

There are several ways to get help:

  • The xAct google group contains a well established, highly active and very friendly community of researchers. Feel free to start a New conversation by posting a minimal working example of your code.
  • For private correspondence, you can email us at barker@fzu.cz.
  • Alternatively you may wish to raise a New issue on GitHub.

Acknowledgements

Hamilcar was improved by many useful discussions with DraΕΎen Glavan and Tom ZΕ‚oΕ›nik.

This work used the DiRAC Data Intensive service (CSD3 www.csd3.cam.ac.uk) at the University of Cambridge, managed by the University of Cambridge University Information Services on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). The DiRAC component of CSD3 at Cambridge was funded by BEIS, UKRI and STFC capital funding and STFC operations grants. DiRAC is part of the UKRI Digital Research Infrastructure.

WB is grateful for the kind hospitality of Leiden University and the Lorentz Institute, and the support of Girton College, Cambridge, Marie SkΕ‚odowska-Curie Actions and the Institute of Physics of the Czech Academy of Sciences.

Last commit:
Thursday, 7 August 2025

View full repository on GitHub β†’
View full repository on GitLab β†’

license arXiv arXiv arXiv Diagram of general relativity field equations from a theoretical physics masters project at Cambridge University.

Hamiltonian Gauge Gravity Surveyor (HiGGS)

Version 1.2.3

  • Feature: abstract indices representing gauge-fixed theory given cleaner formatting with Gothic script, extended indices a1, b1, c1 etc. denoted by primes.
  • Feature: provide more intuitive formatting of Poisson brackets in terms of smearing functions, as seen in output of PoissonBracket and ViewTheory.
  • Patch: fix shadowing error messages during the Needs or Get package call preamble.
  • Patch: fix Issue #1, loading of binaries on Windows.
  • Patch: fix errors produced by PoissonBracket with the option "Surficial"->True. This error follows from sign errors in line two of Equation (E3) in 2205.13534, and generates nonphysical surface terms. My particular thanks to Manuel Hohmann for identifying this.

License

Copyright Β© 2022 Will E. V. Barker

HiGGS is distributed as free software under the GNU General Public License (GPL).

HiGGS is provided without warranty, or the implied warranty of merchantibility or fitness for a particular purpose.

Users of HiGGS, including authors of derivative works as defined by the GPL, are kindly requested to cite the 2022 HiGGS papers (2206.00658 and 2205.13534) in their resulting publications.

These conditions apply to all software in this repository, including β€œHPC-EEG” visualisation tools.

About

HiGGS is an (unofficial) part of the xAct bundle. It provides tools for the Hamiltonian constraint analysis (canoncical analysis or Dirac-Bergmann algorithm) of gravity with spacetime curvature and torsion. HiGGS can be used on a desktop PC, but it is parallelised for theory surveys on clusters and supercomputers.

Installation

Requirements

HiGGS has been tested in the following environment(s):

  • Linux x86 (64-bit), specifically Manjaro, Arch, CentOS, Scientific Linux and Ubuntu
  • Windows 10, as of HiGGS v 1.2.3
  • Mathematica v 11.3.0.0
  • xAct v 1.2.0

    Install

    1. Make sure you have installed xAct.
    2. Download HiGGS: bash, git git clone https://github.com/wevbarker/HiGGS cd HiGGS
    3. Place the ./xAct/HiGGS directory relative to your xAct install. A global install might have ended up at: 
        /usr/share/Mathematica/Applications/xAct

      Quickstart

The package loads just like any other part of xAct, just open a fresh notebook and run:

Needs["xAct`HiGGS`"];

This loads the package (i.e. the names of the functions provided), along with its dependencies in the xAct bundle. However it does not load the physics. To construct the HiGGS environment, one must run:

BuildHiGGS[];

The build process may take about a minute or so. When it has concluded, you should be able to proceed to science. For example, try evaluating the Poisson bracket between the spin-parity 2+ irreducible component of the foliation-projected momentum of the translational gauge field, and the 1- irrep of the foliation-projected torsion tensor, without first defining a constraint shell for a particular theory, type:

PoissonBracket[PiPB2p[-a, -b], TP1m[-c], "ToShell" -> False];

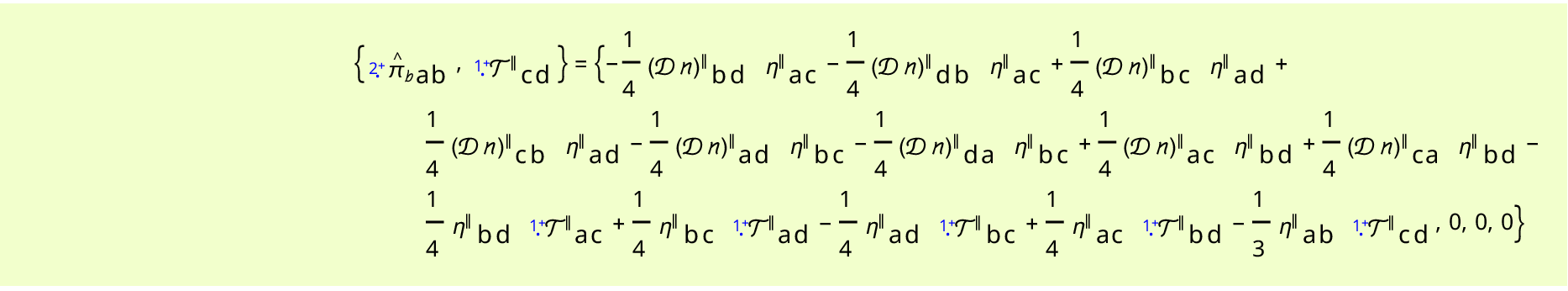
Cambridge theoretical physicist Will Barker's tutorial on general relativity field equations for graduate research.

If you want to try something more ambitious, build the constraint structure for Einstein-Cartan theory:

DefTheory[{Alp1 == 0, Alp2 == 0, Alp3 == 0, Alp4 == 0, Alp5 == 0, 
   Alp6 == 0, Bet1 == 0, Bet2 == 0, Bet3 == 0, cAlp1 == 0, cAlp2 == 0,
    cAlp3 == 0, cAlp4 == 0, cAlp5 == 0, cAlp6 == 0, cBet1 == 0, 
   cBet2 == 0, cBet3 == 0}, "Export" -> "EinsteinCartan"];

That output is less easy to show.

Installation test

More general examples can be found in the notebook ./xAct/HiGGS/Documentation/Examples/tutor.nb. This notebook also acts as an install test.

  1. Move the test files into your working directory, e.g. for a global install: 
     cp /usr/share/Mathematica/Applications/xAct/HiGGS/Documentation/Examples/tutor.nb ./
 cp -r /usr/share/Mathematica/Applications/xAct/HiGGS/Documentation/Examples/svy ./
 mkdir ./fig
  2. Open Mathematica and run ./tutor.nb in a notebook front end. Make sure you run all the initialisation cells, from the beginning, to the end.

What’s in the box?

The HiGGS package has the following structure:

xAct
└── HiGGS
    β”œβ”€β”€ bin
    β”‚Β Β  └── build
    β”‚Β Β      β”œβ”€β”€ CanonicalPhiToggle.mx
    β”‚Β Β      β”œβ”€β”€ CDPiPToCDPiPO3.mx
    β”‚Β Β      β”œβ”€β”€ ChiPerpToggle.mx
    β”‚Β Β      β”œβ”€β”€ ChiSingToggle.mx
    β”‚Β Β      β”œβ”€β”€ CompleteO3ProjectionsToggle.mx
    β”‚Β Β      β”œβ”€β”€ GeneralComplementsToggle.mx
    β”‚Β Β      β”œβ”€β”€ NesterFormIfConstraints.mx
    β”‚Β Β      β”œβ”€β”€ NonCanonicalPhiToggle.mx
    β”‚Β Β      β”œβ”€β”€ O13ProjectionsToggle.mx
    β”‚Β Β      β”œβ”€β”€ ProjectionNormalisationsToggle.mx
    β”‚Β Β      └── VelocityToggle.mx
    β”œβ”€β”€ COPYING
    β”œβ”€β”€ Documentation
    β”‚Β Β  β”œβ”€β”€ Examples
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ appcg.job.m
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ appcg.job.nb
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ appcg.job.sh
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ appcg.plt.py
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ appcg.plt.sh
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ peta4.job.m
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ peta4.job.nb
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ peta4.job.sh
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ peta4.job.slm
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ peta4.plt.py
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ peta4.plt.sh
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ peta4.rdm.png
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ peta4.svy.m
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ peta4.svy.nb
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ svy
    β”‚Β Β  β”‚Β Β  β”‚Β Β  β”œβ”€β”€ EinsteinCartan.thr.mx
    β”‚Β Β  β”‚Β Β  β”‚Β Β  β”œβ”€β”€ EinsteinCartan_vel.thr.mx
    β”‚Β Β  β”‚Β Β  β”‚Β Β  β”œβ”€β”€ simple_spin_1p.thr.mx
    β”‚Β Β  β”‚Β Β  β”‚Β Β  └── simple_spin_1p_vel.thr.mx
    β”‚Β Β  β”‚Β Β  β”œβ”€β”€ tutor.nb
    β”‚Β Β  β”‚Β Β  └── tutor.png
    β”‚Β Β  β”œβ”€β”€ HiGGS.pdf
    β”‚Β Β  └── HiGGS_sources.pdf
    β”œβ”€β”€ HiGGS.m
    β”œβ”€β”€ HiGGS.nb
    β”œβ”€β”€ HiGGS_smearing_functions_global.m
    β”œβ”€β”€ HiGGS_smearing_functions.m
    β”œβ”€β”€ HiGGS_SO3.m
    β”œβ”€β”€ HiGGS_SO3.nb
    β”œβ”€β”€ HiGGS_sources.m
    β”œβ”€β”€ HiGGS_sources.nb
    β”œβ”€β”€ HiGGS_variations.m
    └── Kernel
        └── init.wl

The license is in COPYING.

The file init.wl is called when the package is invoked, and points to HiGGS.m, a small Wolfram language file and main package file sourced by the notebook HiGGS.nb.

When the HiGGS environment is actually built, HiGGS.m is actually running HiGGS_sources.m - the larger β€œphysics package” sourced by HiGGS_source.nb.

During the course of the build, the binaries ./xAct/HiGGS/bin/build/*.mx are incorporated; these contain some heavy expressions.

The sub-package HiGGS_variations.m incorporates elements of Cyril Pitrou’s code from this repository.

The files HiGGS.pdf and HiGGS_sources.pdf are carbon copies of the source notebooks.

The notebook tutor.nb contains some more basic examples, and it relies on the *.thr.mx files in the svy directory.

The Wolfram Language files which refer to smearing functions are patches in version 1.2.2.

What are peta4 and appcg?

The files ./xAct/HiGGS/Documentation/Examples/peta4.* and ./xAct/HiGGS/Documentation/Examples/appcg.* refer to the jobs which implement the HiGGS Commissioning Survey and various unit tests. HiGGS does not need these files to function. The names refer to two computing services:

  1. Peta-4 is a supercomputer, the CPU component of the heterogeneous CSD3 facility belonging to the University of Cambridge.
  2. appcg is a small, private compute server belonging to the Cavendish Laboratory Astrophysics Group.

These sources are included to give inspiration to users who which to perform HPC surveys, though the user’s architecture may well differ.

Contribute

Please do! I’m always responsive to emails (about science), so be sure to reach out at wb263@cam.ac.uk. I will also do my best to get your code working if you are just trying to use HiGGS.

Acknowledgements

This work was performed using resources provided by the Cambridge Service for Data Driven Discovery (CSD3) operated by the University of Cambridge Research Computing Service (www.csd3.cam.ac.uk), provided by Dell EMC and Intel using Tier-2 funding from the Engineering and Physical Sciences Research Council (capital grant EP/T022159/1), and DiRAC funding from the Science and Technology Facilities Council (www.dirac.ac.uk).

I am grateful for the kind hospitality of Leiden University and the Lorentz Institute, and am supported by Girton College, Cambridge.

Last commit:
Tuesday, 31 December 2024

View full repository on GitHub β†’
View full repository on GitLab β†’

license Mathematica xAct

xPlain: Formatting for Mathematical Derivations in Theoretical Physics

Version 0.0.0-developer

License

Copyright Β© 2023 Will E. V. Barker and Sebastian Zell

xPlain is distributed as free software under the GNU General Public License (GPL).

xPlain is provided without warranty, or the implied warranty of merchantibility or fitness for a particular purpose.

If xPlain was useful to your research, please cite us using the following BibTeX:

@misc{Barker:2023xPlain,
    author = "Barker, Will E. V. and Zell, Sebastian",
    title = "{xPlain: Formatting for Mathematical Derivations in Theoretical Physics}",
    year = "2023",
    note = "Part of the xAct bundle"
}

About

xPlain is a software package for Wolfram (formerly Mathematica) designed to format mathematical derivations in theoretical physics. It bridges the gap between programmatic computation and professional presentation by enabling both command-line and notebook interfaces while maintaining consistent, paper-quality mathematical typesetting.

The package addresses a fundamental challenge in theoretical physics: how to simultaneously:

  • Retain the notebook front-end’s mathematical formatting capabilities
  • Present calculations with paper-style layout
  • Work entirely in plaintext using professional development tools

xPlain is an (unofficial) part of the xAct bundle and implements the FAIR guiding principles for scientific data management. It is designed for unambiguous, lasting derivations in the Wolfram Language and is suitable for researchers who use the Wolfram Language programmatically.

The package has been successfully used in published supplemental materials, receiving positive feedback from anonymous referees: β€œIt is remarkable the effort made by the authors with the Supplemental Material to show the connection between the Mathematica code employed for the computations and the statements in the paper.”

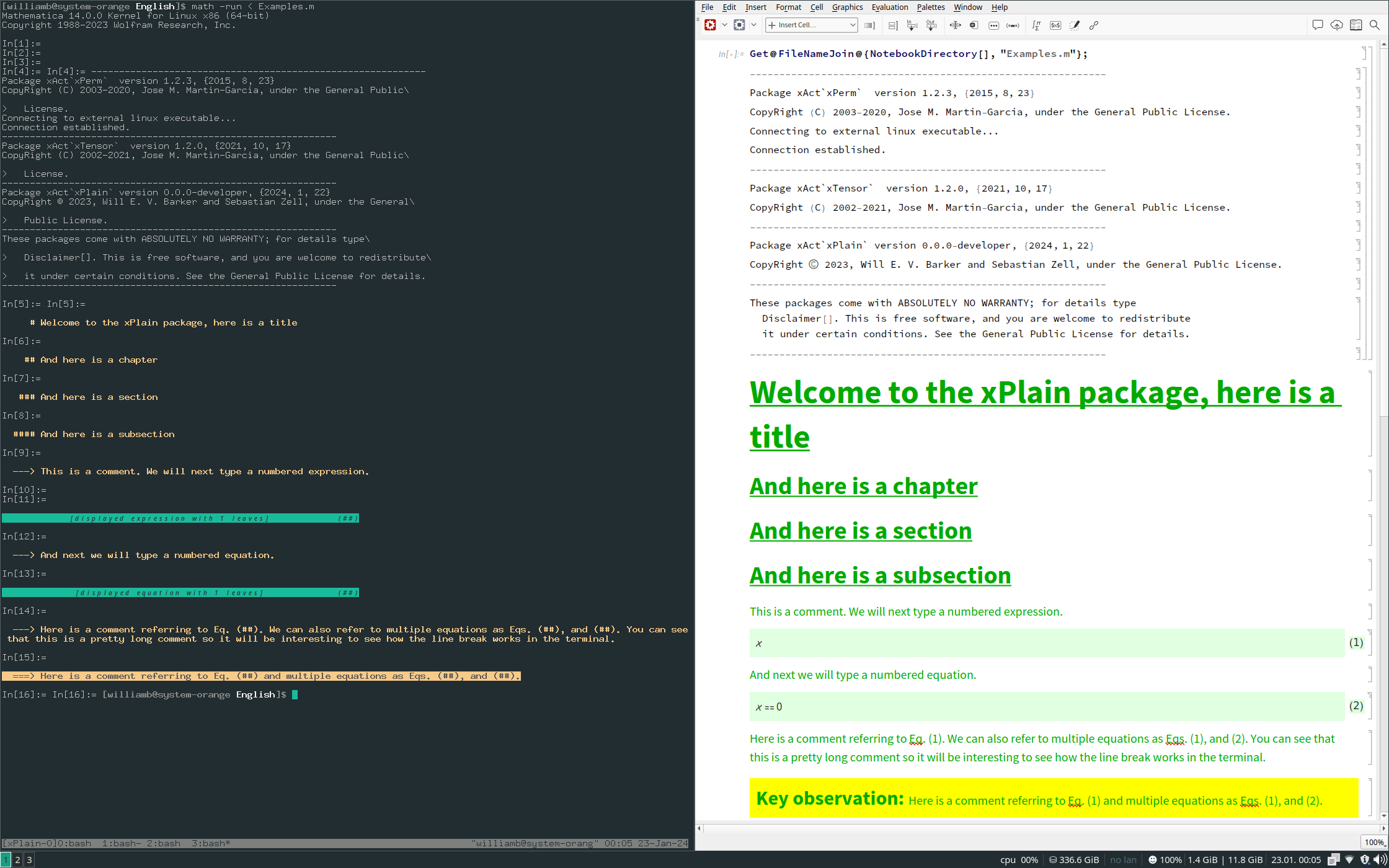
Example: Basic Mathematical Document

As a demonstration, we consider formatting a simple mathematical derivation with sectioning, commentary, and cross-references.

In a fresh notebook we first load the package:

<<xAct`xPlain`;

Next, we create document structure using sectioning commands:

Title@"Welcome to the xPlain package, here is a title";
Chapter@"And here is a chapter";
Section@"And here is a section";
Subsection@"And here is a subsection";

We add commentary and define formatted variables:

Comment@"This is a comment. We will next type a numbered expression.";
Format@xx^=ToExpression@"\[ScriptX]";
DisplayExpression[xx,EqnLabel->"Eq1"];

For expressions that vanish, use the equation environment:

Comment@"And next we will type a numbered equation.";
DisplayEquation[xx,EqnLabel->"Eq2"];

Cross-references are handled automatically:

Comment@{"Here is a comment referring to",Cref@"Eq1",". We can also refer to multiple equations as",Cref@{"Eq1","Eq2"},"."};
Supercomment@{"Here is a comment referring to",Cref@"Eq1"," and multiple equations as",Cref@{"Eq1","Eq2"},"."};

The output is shown below:

Documentation

The package includes a comprehensive example notebook demonstrating all basic functionality. To run the examples:

[user@system xPlain]$ cp xAct/xPlain/Documentation/English/Examples.nb ~/Examples.nb
[user@system xPlain]$ cd ~
[user@system ~]$ wolframnb Examples.nb &

General use

Document Structure

The package provides hierarchical sectioning commands:

  • Title["title text"] - Document title
  • Chapter["chapter text"] - Chapter heading
  • Section["section text"] - Section heading
  • Subsection["subsection text"] - Subsection heading

Commentary and Display

  • Comment["text"] or Comment[{"text", Cref["label"], "more text"}] - Regular commentary with optional cross-references
  • Supercomment[...] - Emphasized commentary
  • DisplayExpression[expr, EqnLabel->"label"] - Numbered mathematical expression
  • DisplayEquation[expr, EqnLabel->"label"] - Numbered equation (implies vanishing)

Cross-referencing

  • Cref["label"] - Reference to a single equation
  • Cref[{"label1", "label2"}] - Reference to multiple equations
  • Mref["label"] - Alternative reference format

Mathematical Formatting

Format variables using standard Wolfram Language conventions:

Format@myvar^=ToExpression@"\[ScriptM]";

Quickstart

Requirements

Basic hardware requirements

  • A multi-core processor (recommended)
  • An internet connection (recommended for package dependencies)

Operating systems

Software dependencies

Installation

:warning: Note that Mathematica was re-branded as Wolfram on July 31 2024 with the release of Wolfram v 14.1. You may still be able to install xPlain in older versions by replacing Wolfram with Mathematica in the paths below.

Linux

  1. Prepare. Make sure your system satisfies all the requirements.
  2. Download. Clone or download the repository: 
    [user@system ~]$ git clone https://github.com/wevbarker/xPlain
  3. Install. Use the provided installation script: 
    [user@system xPlain]$ ./install.sh

    Alternatively, manually copy to your xAct installation:

    [user@system xPlain]$ cp -r xAct/xPlain ~/.Wolfram/Applications/xAct/

    For a global installation:

    [user@system xPlain]$ sudo cp -r xAct/xPlain /usr/share/Wolfram/Applications/xAct/

macOS

  1. Prepare. Make sure your system satisfies all the requirements.
  2. Download. Clone or download the repository: 
    user@system ~ % git clone https://github.com/wevbarker/xPlain
  3. Install. Copy to your xAct installation: 
    user@system xPlain % cp -r xAct/xPlain ~/Library/Mathematica/Applications/xAct/

    For a global installation:

    user@system xPlain % sudo cp -r xAct/xPlain /Library/Mathematica/Applications/xAct/

Microsoft Windows

  1. Prepare. Make sure your system satisfies all the requirements.
  2. Download. Clone or download the repository: 
    C:\Users\user> git clone https://github.com/wevbarker/xPlain
  3. Install. Copy to your xAct installation: 
    C:\Users\user\xPlain> xcopy /e /k /h /i xAct\ "C:\Users\user\AppData\Roaming\Mathematica\Applications\xAct\"

    For a global installation (run as administrator):

    C:\Users\user\xPlain> xcopy /e /k /h /i xAct\ "C:\Program Files\Wolfram Research\Mathematica\14.0\AddOns\Applications\xAct\"

Getting help

There are several ways to get help:

  • The xAct google group contains a well-established, highly active and very friendly community of researchers. Feel free to start a New conversation by posting a minimal working example of your code.
  • For private correspondence, you can email us at wb263@cam.ac.uk.
  • You may wish to raise a New issue on GitHub.

Acknowledgements

This work was performed using resources provided by the Cambridge Service for Data Driven Discovery (CSD3) operated by the University of Cambridge Research Computing Service (www.csd3.cam.ac.uk), provided by Dell EMC and Intel using Tier-2 funding from the Engineering and Physical Sciences Research Council (capital grant EP/T022159/1), and DiRAC funding from the Science and Technology Facilities Council (www.dirac.ac.uk).

I am grateful for the kind hospitality of Leiden University and the Lorentz Institute, and am supported by Girton College, Cambridge.

Last commit:
Monday, 25 August 2025

View full repository on GitHub β†’
View full repository on GitLab β†’

license Mathematica

NoMoreNotebooks: Programmatic Wolfram Notebook Interface

Version 14.2

  • Updated for Wolfram Language 14.2 compatibility
  • Added support for both Wolfram and Mathematica FrontEnd commands
  • Enhanced non-interactive mode for batch processing

License

Copyright Β© 2024 Will Barker

NoMoreNotebooks is distributed as free software under the GNU General Public License (GPL).

NoMoreNotebooks is provided without warranty, or the implied warranty of merchantibility or fitness for a particular purpose.

If NoMoreNotebooks was useful to your research, please consider citing this work.

About

NoMoreNotebooks is a software package for Wolfram (formerly Mathematica) designed to provide a programmatic interface to Wolfram notebooks. It enables running Wolfram Language code through a FrontEnd connection while maintaining complete control over notebook creation, evaluation, and output generation.

The package allows you to:

  • Create and manipulate notebooks programmatically
  • Execute Wolfram Language files in notebook environments
  • Export notebook contents to various formats
  • Control evaluation flow and timing
  • Work in both interactive and batch processing modes

Example: Basic workflow

In a fresh notebook or kernel session, load the package:

<<NoMoreNotebooks`;

Establish a FrontEnd connection and create a target notebook:

Ignite[]

Load and execute a Wolfram Language file in the notebook:

Burn["myfile.m"]

Export the notebook to a file:

Singe["output.pdf"]

Close the notebook when finished:

Douse[]

Core Functions

Ignite[]

Establishes a FrontEnd connection and creates a target notebook with dark theme styling. This must be called before any other operations.

Burn[filename]

Loads and executes a .m file in the target notebook. The file is evaluated and the results are displayed in the notebook. The corresponding .nb file is automatically saved.

Douse[]

Closes the target notebook and cleans up the FrontEnd connection.

Singe[filename]

Exports the current notebook contents to the specified file format (typically PDF).

Smother[]

Aborts the current evaluation in the target notebook.

VimJ[]

Navigation helper that moves to the next cell in the notebook.

Configuration Variables

The package behavior can be customized through several global variables:

  • $NonInteractive: Set to True for batch processing mode (default: False)
  • $TargetKernelName: Kernel name for evaluation (default: "NoMoreNotebooks")
  • $DeletePauseTime: Delay time for cell operations in seconds (default: 10)

Quickstart

Requirements

Basic hardware requirements

  • A multi-core processor (recommended for better performance)
  • Sufficient memory for Wolfram Language operations

Operating systems

  • Linux (recommended, tested on various distributions)
  • macOS (supported)
  • Windows (supported)

Software dependencies

Installation

:warning: Note that Mathematica was re-branded as Wolfram on July 31 2024 with the release of Wolfram v 14.1. The package automatically detects your version and uses the appropriate commands.

Installation via script

  1. Download. Clone or download this repository to your local system.

  2. Install. Run the provided installation script:

    ./install.sh

This will copy the package to both ~/.Wolfram/Applications/ and ~/.Mathematica/Applications/ directories, ensuring compatibility with both new and legacy installations.

Manual installation

Alternatively, you can manually copy the NoMoreNotebooks/ directory to your Wolfram Applications directory:

Linux/macOS:

cp -r NoMoreNotebooks ~/.Wolfram/Applications/
cp -r NoMoreNotebooks ~/.Mathematica/Applications/  # For legacy versions

Windows: Copy the NoMoreNotebooks/ folder to:

  • C:\Users\[username]\AppData\Roaming\Mathematica\Applications\
  • C:\Users\[username]\AppData\Roaming\Wolfram\Applications\

Version Compatibility

The package automatically adapts to your Wolfram Language version:

  • Version ≀ 14.0: Uses mathematica command for FrontEnd launch
  • Version > 14.0: Uses wolframnb command for FrontEnd launch

Interactive vs Non-Interactive Modes

Interactive Mode (default):

  • Provides user feedback and status messages
  • Includes timing delays for cell operations
  • Suitable for development and testing

Non-Interactive Mode ($NonInteractive = True):

  • Optimized for batch processing
  • Minimal output and faster execution
  • Waits for file operations to complete automatically

Use Cases

NoMoreNotebooks is particularly useful for:

  • Batch processing: Running multiple Wolfram Language files systematically
  • Automated reporting: Generating formatted notebook outputs programmatically
  • Testing and validation: Running code in controlled notebook environments
  • Documentation generation: Creating formatted mathematical documents
  • Educational tools: Automating notebook creation for teaching materials

Getting Help

If you encounter issues or have questions:

  • Check the function documentation within Wolfram Language using ?FunctionName
  • Ensure your Wolfram installation is properly configured
  • Verify that the FrontEnd can be launched from your system
  • For bug reports, please include your Wolfram version and operating system details

Development Notes

  • The package requires a functional Wolfram FrontEnd installation
  • FrontEnd connection is essential for all notebook operations
  • The package handles version differences automatically
  • Dark theme styling is applied by default for better visibility
  • File operations include automatic saving and cleanup
Last commit:
Wednesday, 6 August 2025

View full repository on GitHub β†’
View full repository on GitLab β†’

License: MIT

Martensite Banner

Martensite

Adversarial hardening for modern grantsmanship

Logos (this part was written by a human)

Grantsmanship - the process of securing grants - is changing due to AI. This is an unprecedented, irreversible and unavoidable process, occurring at a rate which exceeds the adaptive capacity of all institutions and most individuals. From the accelerationist perspective, it is necessary to lean in to emerging technologies and ensure that they serve to maximise scientific productivity. This is, moreover, a duty incumbent on all researchers, owing to the importance of public trust in the academic enterprise.

Within Europe, applications for prestigious funding opportunities have risen sharply since 2022. Applicants are using LLMs to craft and refine their proposals, and referees are using LLMs to evaluate them. A minority of both applicants and referees deny this, including a dwindling subset who are telling the truth. Considering only the tools that are available at the time of writing, academia will naturally saturate in a configuration where LLM-assisted grantsmanship is not only ubiquitous, but also acceptable, and even expected. It will be argued elsewhere that this will have several benefits, including but not limited to:

  • The liberation of time which can be spent on research, constituting a better use of public money.
  • Mitigation of disadvantages which are utterly irrelevant to caliber of the researcher, such as being a non-native English speaker.
  • Improved signal-to-noise ratio in gauging the excellence of ideas, due to all proposals having - and being expected to have - flawless presentation.
  • A general diminution of grantsmanship itself as a proxy metric, and a return to results-based evaluation: β€œStop promising to do things. What did you publish with your last grant, and who cited you?”

Martensite is intended to bring this saturation point forwards in time. The source code should be cloned, forked, or used a prompt for those wishing to roll their own system. The name derives from the hard, strong crystalline phase of steel formed by rapid quenching.

martensite -a application.pdf -c call_dir -P "I have been tasked with reviewing this research proposal, which is slightly outside of my area of expertise. Can you carefully examine the call text, and read the proposal, and draft a review for me?" -o report.pdf

Takes your research proposal application.pdf and the public call texts downloaded to call_dir, and generates multiple referee reports in report.pdf. The prompt is sent to the most advanced flagship models from OpenAI, Anthropic, and Google. You will need to have funded API keys for at least one provider.

Quick Start

For confident super-users. If you’re less comfortable in the terminal, proceed step-by-step through Installation below.

# Install dependencies
pip install -r requirements.txt

# Run a review with inline prompt
martensite -a application.pdf -P "Review this carefully"

# Run with call documentation
martensite -a application.pdf -c CallTexts/ -P "Review against these criteria"

# Run with custom output location
martensite -a CV.pdf -P "Focus on research impact" -o cv_review.pdf

Installation

1. PATH Configuration

The PATH tells your terminal where to find commands. This step lets you type martensite from any directory instead of typing the full path to the program.

Add Martensite to your PATH using either method:

Option A: Direct export

This adds Martensite to your PATH permanently.

# Add this line to your ~/.bashrc or ~/.zshrc
export PATH="$PATH:/path/to/Martensite"

# Reload your shell configuration
source ~/.bashrc  # or source ~/.zshrc

Option B: Symbolic link

This creates a shortcut in a directory that’s already in your PATH.

ln -s /path/to/Martensite/martensite.sh ~/.local/bin/martensite

2. Dependencies

Martensite is written in Python and generates referee reports as PDF files. You’ll need to install some additional software packages.

Python dependencies:

These are Python libraries that Martensite uses to communicate with AI providers and process documents.

pip install -r requirements.txt

Report dependencies:

PDF generation requires pandoc (document converter), LaTeX (typesetting system), and PDF utilities.

Linux (Arch/Manjaro):

sudo pacman -S pandoc texlive-core texlive-latexextra poppler

Linux (Debian/Ubuntu):

sudo apt install pandoc texlive-xetex texlive-latex-extra poppler-utils

macOS:

brew install pandoc poppler
brew install --cask mactex  # Or: brew install texlive

3. API Keys

Martensite supports three LLM providers. You need at least one API key to run reviews.

What are API keys?

If you’ve used ChatGPT through a web browser, you’ve been using OpenAI’s consumer interface. API keys let Martensite access the same AI models programmatically, directly from your computer. Unlike the web interface with a monthly subscription, API access is pay-as-you-go: you add funds to your account and pay only for what you use (typically a few cents per review). You’ll need to create a developer account with at least one provider (OpenAI, Anthropic, or Google) and add payment information before generating API keys.

How Martensite finds your keys:

Martensite checks three locations in order: environment variables β†’ OS keyring β†’ config file. Choose whichever method is most convenient for you.

Option A: Environment variables (recommended)

export OPENAI_API_KEY="sk-..."
export ANTHROPIC_API_KEY="sk-ant-..."
export GOOGLE_API_KEY="..."

Option B: OS keyring

# Uses system Keychain (macOS) or Secret Service (Linux)
keyring set llm/openai default    # paste key when prompted
keyring set llm/anthropic default
keyring set llm/google default

Option C: Config file

Create ~/.config/llm-keys/config.toml (Linux) or ~/Library/Application Support/llm-keys/config.toml (macOS):

[openai]
api_key = "sk-..."

[anthropic]
api_key = "sk-ant-..."

[google]
api_key = "..."

Platform Support

  • Linux: Fully supported (tested on Arch, Ubuntu, Debian)
  • macOS: Fully supported (10.15+ recommended)

Usage

Basic Review

martensite -a StatementOfPurpose.pdf -P "Review this research proposal"

With Call Documentation

martensite -a proposal.pdf -c CallTexts/ -P "Evaluate against call criteria"

Custom Output Path

martensite -a CV.pdf -P "Focus on career progression" -o reviews/cv_review.pdf

Dry Run (Testing)

martensite -a proposal.pdf -P "Test prompt" -o test.pdf -d

Command-Line Options

  • -a, --application: Path to PDF application file (required)
  • -p, --prompt: Path to text file containing review prompt
  • -P, --prompt-string: Review prompt as inline string
  • -c, --call-docs: Path to directory or PDF with call documentation
  • -o, --output: Output path for generated PDF (default: martensite.pdf)
  • -d, --dry-run: Skip API calls and generate dummy reviews for testing
  • -h, --help: Show help message

Project Structure

Martensite/
β”œβ”€β”€ martensite/              # Core Python package
β”‚   β”œβ”€β”€ __init__.py
β”‚   β”œβ”€β”€ key_discovery.py     # Secure API key management
β”‚   β”œβ”€β”€ application_reviewer.py  # Multi-LLM orchestration
β”‚   β”œβ”€β”€ martensite_handler.py    # CLI backend handler
β”‚   └── extract_pdf_text.py # PDF text extraction utilities
β”œβ”€β”€ tests/                   # Test suite
β”‚   β”œβ”€β”€ LaCaixaIASTRO/      # Test application files
β”‚   └── *.sh                # Test scripts
β”œβ”€β”€ martensite.sh           # Main CLI entry point
β”œβ”€β”€ requirements.txt        # Python dependencies
└── README.md               # This file

Core Components

1. Multi-LLM Orchestration (application_reviewer.py)

  • Parallel API calls across OpenAI, Anthropic, and Google models
  • Configurable model selection for diverse perspectives
  • PDF processing with text extraction
  • Async execution for maximum performance
  • Comprehensive error handling and retry logic

2. Secure Key Management (key_discovery.py)

  • Environment variables checked first
  • System keyring integration (keyctl/Keychain)
  • XDG config directory fallback (~/.config/martensite/)
  • Multi-provider support for OpenAI, Anthropic, Google

3. CLI Handler (martensite_handler.py)

  • Argument parsing and validation
  • PDF text extraction using PyPDF2
  • Markdown generation with structured output
  • PDF conversion via pandoc/XeLaTeX
  • Token usage reporting

Supported Models

OpenAI

  • GPT-5: Most advanced reasoning model
  • GPT-4o: Flagship multimodal model
  • o4-mini-2025-04-16: Cost-effective reasoning model

Anthropic

  • claude-sonnet-4-5-20250929: Latest flagship model

Google

  • gemini-2.5-pro: Advanced multimodal model

Troubleshooting

β€œCommand not found”: Check your PATH or use full path to martensite.sh

PDF extraction fails: Install PyPDF2 (pip install PyPDF2)

PDF conversion fails:

  • Linux: sudo apt install pandoc texlive-xetex or sudo pacman -S pandoc texlive-core
  • macOS: brew install pandoc and brew install --cask mactex

Unicode errors: Ensure XeLaTeX is installed with Unicode font support

API key not found:

  • Set environment variables: export OPENAI_API_KEY=sk-...
  • Or use OS keyring: keyring set llm/openai default (then paste key)
  • Or create config file:
    • Linux: ~/.config/llm-keys/config.toml
    • macOS: ~/Library/Application Support/llm-keys/config.toml

Model fails: Check API call log in output for specific error messages

macOS: β€œOperation not permitted”: Grant Terminal full disk access in System Preferences β†’ Security & Privacy

License

See LICENSE file for details.

Acknowledgements

I am indebted to Will Handley for (i) calling out zero-sum famine mentality on my part, and encouraging me to make this repository public, and (ii) funding the OpenAI inference used during development. I am also grateful to Ilona GottwaldovΓ‘ for bringing the big picture of LLM-assisted grantsmanship to my attention.

Last commit:
Wednesday, 8 October 2025

View full repository on GitHub β†’
View full repository on GitLab β†’

License: MIT

Sauron Banner

Sauron

AI-powered academic collaborator discovery for theoretical physics

python rank_collaborators.py "Perimeter Institute for Theoretical Physics"

Automatically discovers researchers at target institutions, analyzes their publication history, and ranks them by compatibility with your research program using AI-powered analysis.

Overview

Academic collaboration requires identifying researchers whose work aligns with your research interests and future directions. Sauron automates this process by:

  1. Discovering researchers at target institutions using web search and INSPIRE HEP profiles
  2. Gathering publication metadata (titles, abstracts, citations) via INSPIRE API
  3. Analyzing research compatibility using large context window models (Gemini 2.5 Pro)
  4. Ranking potential collaborators based on both existing overlap and future research directions

The system is designed for theoretical physicists working in high-energy physics, cosmology, astrophysics, and related fields where INSPIRE HEP provides comprehensive publication coverage.

Quick Start

For confident users familiar with Python and API keys.

# Install dependencies
pip install -r requirements.txt

# Set API keys
export OPENAI_API_KEY="sk-..."
export GOOGLE_API_KEY="..."

# Run full pipeline for an institution
python rank_collaborators.py "Stanford Applied Physics"

# Limit to top 10 researchers
python rank_collaborators.py "Kavli Institute Cambridge" -n 10

Installation

1. Dependencies

Python requirements:

pip install -r requirements.txt

Required packages:

  • requests - INSPIRE API queries
  • google-generativeai - Gemini 2.5 Pro ranking
  • openai - GPT-4o web search for researcher discovery

2. API Keys

Sauron requires API keys from two providers:

OpenAI (researcher discovery via web search):

export OPENAI_API_KEY="sk-..."

Google (collaboration ranking via Gemini 2.5 Pro):

export GOOGLE_API_KEY="..."

Martensite integration (optional):

If you have Martensite installed, Sauron will automatically use its key discovery system, which supports environment variables, OS keyring, and config files.

3. Personal Context

To rank collaborators, Sauron needs your research context:

Your papers (LaTeX sources from arXiv):

cd Self/
./download_papers.sh  # Downloads all your papers from INSPIRE
./GatherSelf.sh       # Extracts main .tex files

Your applications (2025 job applications):

Place your application .tex files in ~/Documents/Applications/2025/, then:

cd ~/Documents/Applications/Generics/
./GatherContext.sh    # Gathers application context

Combined context:

./GatherSelfCombined.sh  # Combines papers + applications (~800k tokens)

Usage

Full Pipeline

# Analyze all researchers at an institution
python rank_collaborators.py "Perimeter Institute"

# Limit analysis to first N researchers (faster, cheaper)
python rank_collaborators.py "University of Chicago KICP" -n 15

# Specify custom output directory
python rank_collaborators.py "Cambridge DAMTP" -o output/cambridge/

Individual Stages

Stage 1: Find researchers

python find_researchers.py "Stanford Applied Physics"
# Output: Stanford_Applied_Physics_researchers.md

Stage 2: Gather papers for a specific researcher

./gather_author.sh William.E.V.Barker.1 output.md

Stage 3-4: Ranking (requires combined context and researcher papers)

python rank_collaborators.py "Institution Name"

How It Works

1. Researcher Discovery

Uses OpenAI GPT-4o with web search to:

  • Find institution faculty/researcher pages
  • Extract researcher names
  • Query INSPIRE HEP API for profile matches
  • Expand results using INSPIRE affiliation data

INSPIRE expansion: After initial name matching, Sauron queries INSPIRE for all current researchers at the institution’s INSPIRE-registered IDs, dramatically improving coverage.

2. Paper Gathering

For each researcher with an INSPIRE profile:

  • Queries INSPIRE API for 30 most recent papers
  • Extracts: title, authors, journal, citations, abstract
  • Compact representation (~330 tokens/paper)

3. Context Building

Combines:

  • Your papers: 20 most recent LaTeX sources (~620k tokens)
  • Your applications: 2025 research statements and applications (~185k tokens)
  • Collaborator papers: Titles and abstracts (~195k token budget)

Total: <1M tokens (fits within Gemini 2.5 Pro context window)

4. AI Ranking

Sends combined context to Gemini 2.5 Pro with a prompt that evaluates:

Existing overlap: Do they work on topics related to your past publications?

Future direction alignment: Do they have expertise in areas you’re planning to move into (from your research statements)?

This dual criterion ensures high rankings for both:

  • Researchers with immediate topical overlap (easy collaboration)
  • Researchers with skills you want to learn (strategic collaboration)

Output Format

Rankings are saved as output/INSTITUTION_NAME/ranking.md:

1. [Researcher Name] - INSPIRE_BAI
   **Research overlap:** [1-2 sentence summary]
   **Collaboration potential:** [Assessment]
   **Recommendation:** [Based on existing overlap / future direction / both]

2. [Next researcher...]

Project Structure

Sauron/
β”œβ”€β”€ find_researchers.py       # Stage 1: OpenAI + INSPIRE discovery
β”œβ”€β”€ gather_author.sh          # Stage 2: INSPIRE paper metadata
β”œβ”€β”€ rank_collaborators.py     # Stages 3-4: Full pipeline orchestration
β”œβ”€β”€ GatherSelfCombined.sh     # Build your context (papers + applications)
β”œβ”€β”€ Self/                     # Your arXiv papers (LaTeX sources)
β”‚   β”œβ”€β”€ download_papers.sh
β”‚   β”œβ”€β”€ GatherSelf.sh
β”‚   └── [arxiv_id]/
β”œβ”€β”€ output/                   # Generated results (gitignored)
β”‚   └── [institution]/
β”‚       β”œβ”€β”€ ranking.md
β”‚       β”œβ”€β”€ ranking_context.md
β”‚       └── *.papers.md
└── README.md

Token Budget

Gemini 2.5 Pro has a 1M token context window. Typical usage:

Component Tokens
Your papers (20 recent) ~620k
Your applications (2025) ~185k
Subtotal (your context) ~805k
Available for collaborators ~195k
Collaborators analyzed ~50-60

Cost Estimates

Per institution analysis (assuming ~50 researchers):

  • OpenAI GPT-4o (web search): ~$0.50
  • INSPIRE API: Free
  • Gemini 2.5 Pro (ranking): ~$5.00

Total: ~$5.50 per institution

Platform Support

  • Linux: Fully supported (tested on Arch)
  • macOS: Compatible (requires bash, Python 3.8+)

Limitations

  • INSPIRE coverage: Only finds researchers with INSPIRE HEP profiles (theoretical physics, cosmology, HEP)
  • Token budget: Limited to ~50-60 researchers per ranking due to 1M token window
  • Accuracy: Web search quality depends on institution website structure
  • Recency: INSPIRE data may lag recent appointments by weeks/months

Troubleshooting

No researchers found: Institution may have non-standard website structure or researchers may not be in INSPIRE

Token limit exceeded: Reduce -n parameter or analyze fewer researchers

INSPIRE API timeout: Add delay between requests (edit gather_author.sh)

Gemini API error: Check GOOGLE_API_KEY and account quota

Roadmap

  • Support for additional databases (ADS, arXiv author search)
  • ORCID integration for non-HEP researchers
  • Batch processing for multiple institutions
  • Citation network analysis
  • Email template generation

License

See LICENSE file for details.

Ethics

This tool is intended for professional academic networking and job market research. It should:

  • Help early-career researchers identify compatible mentors and collaborators
  • Reduce geographic and social barriers in academic networking
  • Assist in targeted, thoughtful outreach (not spam)

It should not be used for:

  • Mass unsolicited emails
  • Circumventing normal academic channels
  • Research evaluation or hiring decisions without human review

Responsible use means reading the papers, engaging thoughtfully, and respecting researchers’ time.

Last commit:
Saturday, 25 October 2025

View full repository on GitHub β†’