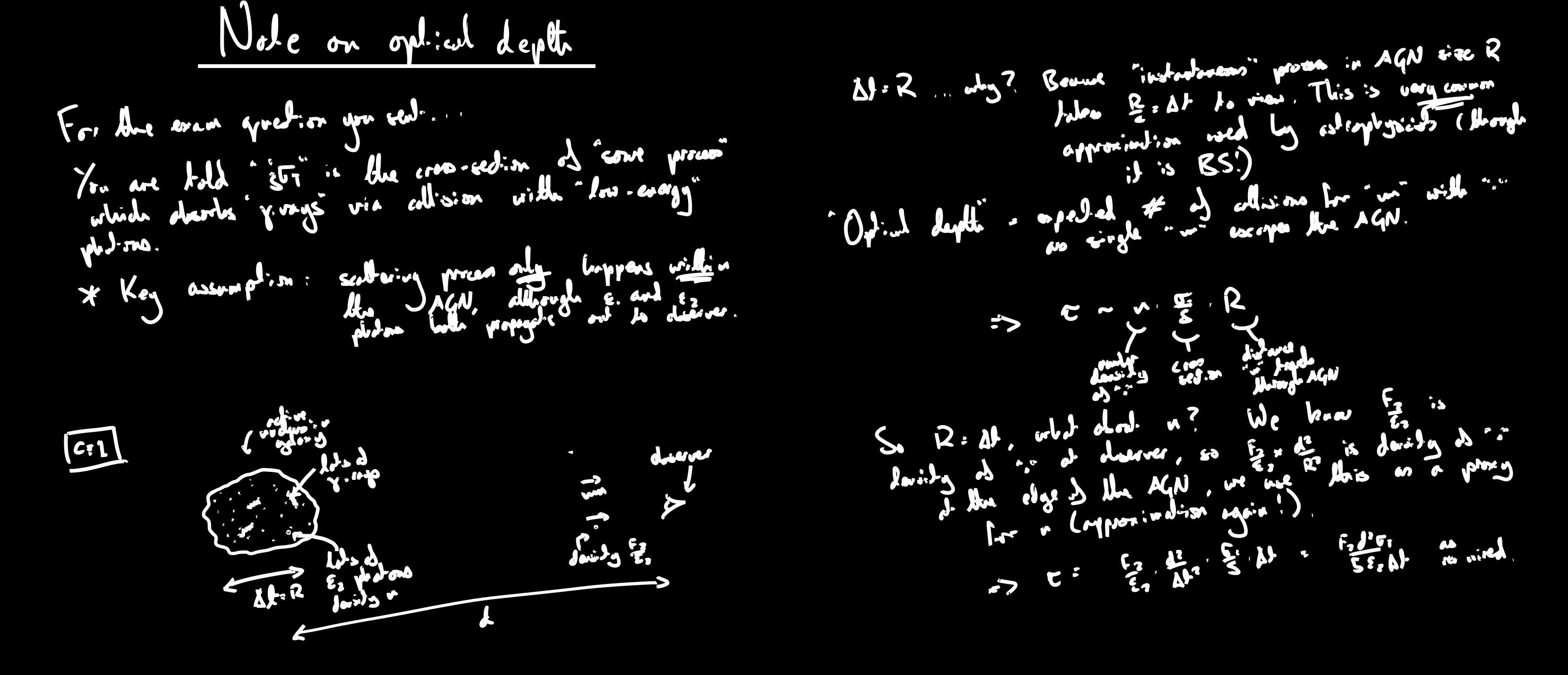Undergraduate teaching
This page is a "clearinghouse" for blackboards and other resources collected from undergraduate teaching. Most of these resources were developed during my work as College Lecturer in Astrophysics for Girton College, Cambridge. For teaching I mostly use a Linux-compatible stylus.
Condensed Matter Physics Top
The "Condensed matter physics" course introduces some ultra-low-energy effective theories, particularly those which we commonly encounter in our narrowly-defined regime of existence well below the Planck scale. In this regime it is proposed that there are such things as crystals, with their periodic lattices giving rise to reciprocal space, Brillouin zones, and the fascinating world of band theory. Among them are metals: these are actually interesting, and give rise to such interesting models as Fermi liquid theory, though you will not learn about this in the present course. The course covers phonons as quantized lattice vibrations, the distinction between acoustic and optical modes, and the emergence of effective mass in crystalline environments. Electronic band structure, semiconductor physics, and the basics of p-n junctions are explored through tight-binding models and nearly-free electron approximations. Some of you may find this course interesting, but beware: the correct route of entry into the condensed matter world is via the quantum dynamics/TP route which is on offer in Part II. Basically, if the course is designed and run by someone at the TCM group, then it can be trusted, but otherwise you should be suspicious!
Lecture 5 Top
Matrix mechanics and hybridisation for a double potential well, exploring tunnel splitting and symmetric/antisymmetric state formation. Spin-orbit interaction as a relativistic correction to the Hamiltonian, arising from the electron's motion through the nuclear electric field. Energy level splitting in the quantum harmonic oscillator due to perturbative corrections and anharmonic terms. Application of degenerate perturbation theory and the construction of appropriate basis states. Connection to molecular orbital theory and the formation of bonding/antibonding states (this feels incorrect to me, please check).
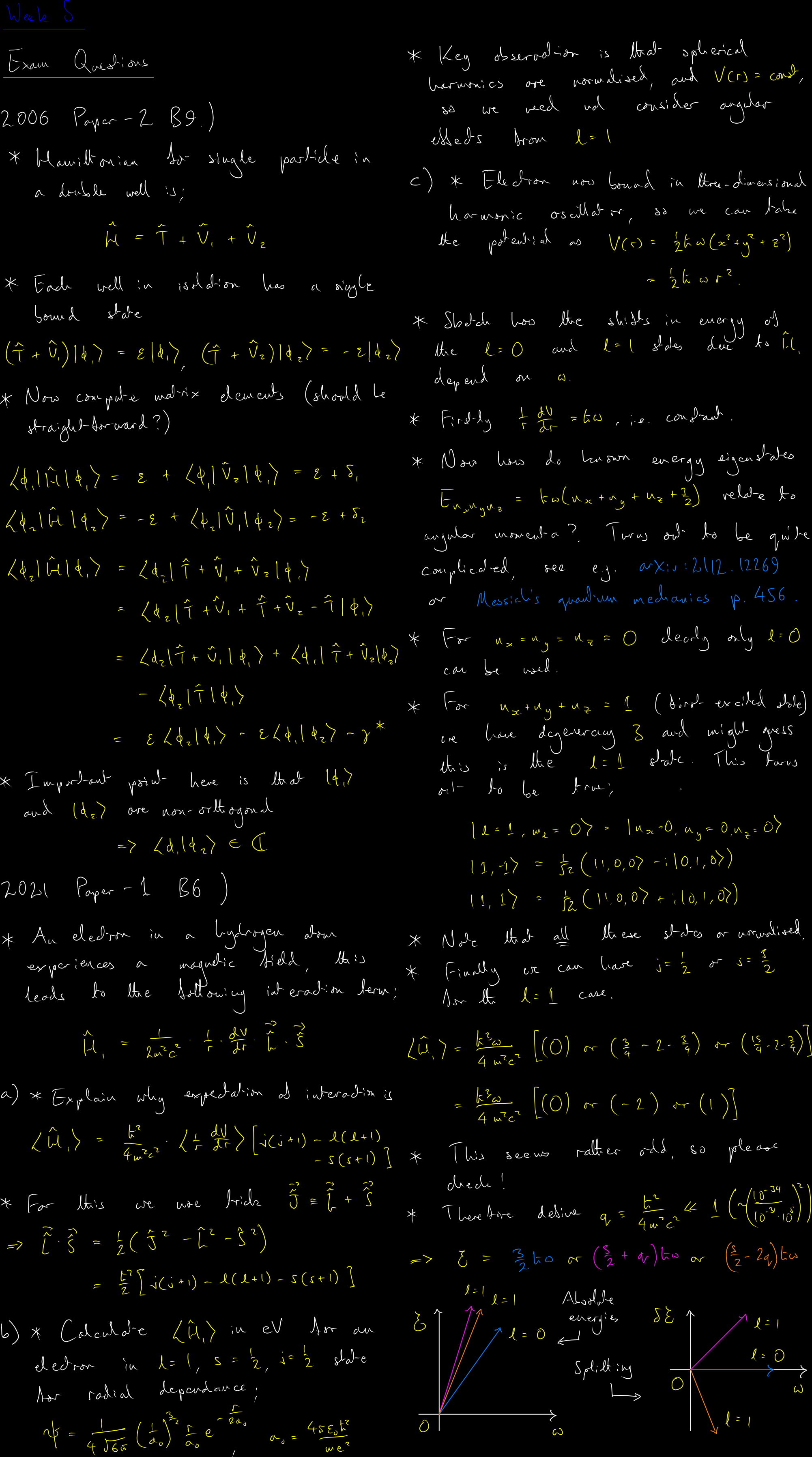
Lecture 4 Top16:00-18:00 Mon. 22nd May 2023
Please remember that this one will be online! -- (and it was online!)
Bloch's theorem and quantisation in a periodic background potential, valence and conduction bands, band splitting, valence and metallic/insulator character, hole states, effective and anisotropic mass, dopants and effective hydrogen-like states within insulators, semiconductors, p/n junctions, potential bias, recombination current.

Factorisation of spatial and spin states of indistinguishable particle pairs, spatial exchange symmetry and Coulombic pair-interaction, Bloch's ansatz for the periodic ring potential.
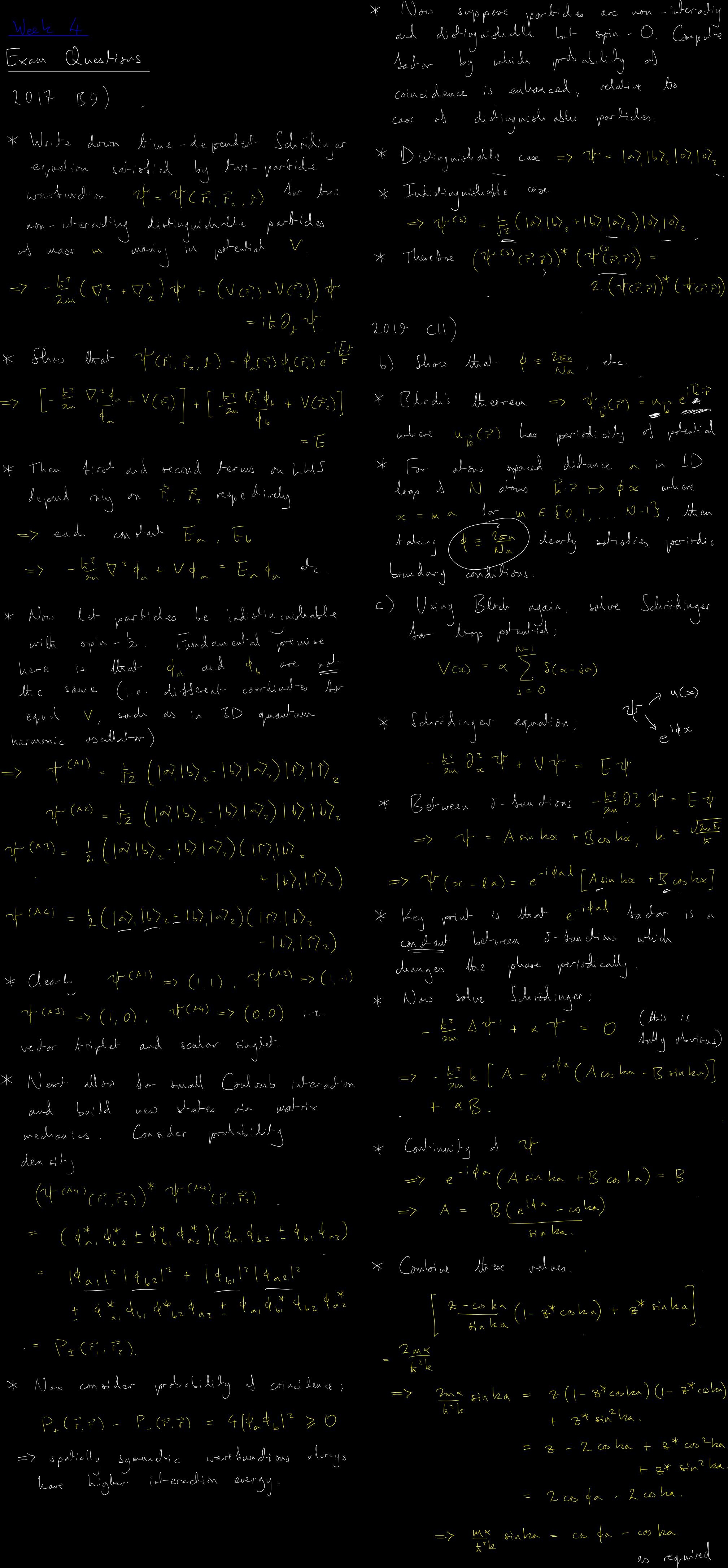
Lecture 3 Top14:00-16:00 Mon. 17th May 2023
Unfortunately, the deadline for my Master's students to submit their theses was at 16:00 BST today, and that led to a few (perfectly avoidable) crises throughout the morning. As a result, I failed to solve this week's solutions within my usual morning window. It is very unlikely I will return to this now, so please let me know if any of the problems need attention!
Lecture 2 Top14:00-16:00 Mon. 8th May 2023
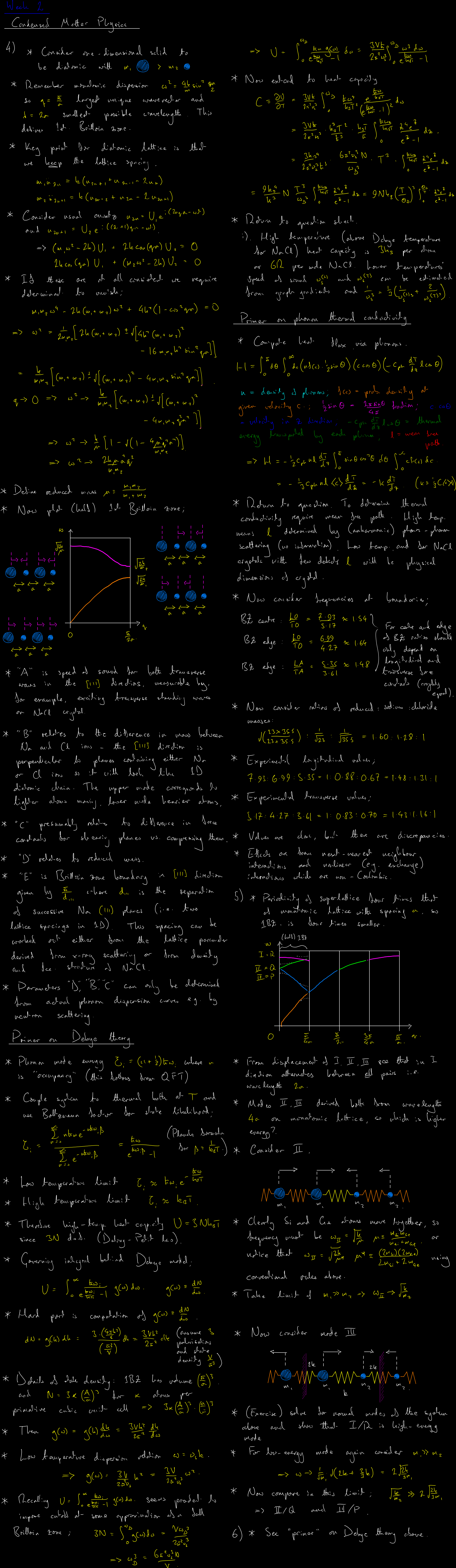
Diatomic phonon dispersion relations, reduced periodicity and folding of the Brilloin zone, splitting of acoustic and optical modes, crystal momentum. Debye theory, Dulong-Petit law, Planck distribution, bosonic occupancy of phonon modes, phonons as non-relativistic quantum field theories, phonon dispersion relations of sodium chloride and a silicon germanium superlattice, using normal mode intuition and reduced masses to infer splitting hierarchies.
Lecture 1 Top15:00-16:00 Thur. 27th Apr. 2023
Please remember that this one will be online! -- (and it was online!)
Introduction to the Bravais lattice as the fundamental geometric structure underlying crystalline solids. Crystallographic groups and symmetry operations that classify crystal structures. Miller indices for describing crystal planes and directions in three-dimensional lattices. Unit cells and primitive cells as the minimal repeating units that generate the entire crystal. The reciprocal lattice as the Fourier transform of the real space lattice, crucial for understanding diffraction and electronic band structure. Monatomic phonon theory in one dimension, treating lattice vibrations as quasiparticle excitations with quantized energy and momentum.

Quantum Physics Top
The "Quantum physics" course offers an introduction to the non-relativistic quantum theory, covering fundamental concepts from wave-particle duality to angular momentum quantization. Little or no attention is given to the axioms of quantum theory or measurement postulates. Lots of emphasis is placed on the position ("wave function" or "quantum wave") representation for massive particles, exploring the Schrödinger equation in coordinate space, which is not a great basis for learning quantum field theory (QFT) next year (it is useful for applications within quantum chemistry and experimental solid state physics). The course introduces bound state problems including infinite and finite square wells, the quantum harmonic oscillator with creation/annihilation operators, and the hydrogen atom via spherical coordinates. There is an introduction to the quantisation of orbital and intrinsic angular momentum, covering ladder operators, Clebsch-Gordan coefficients, spin statistics, and the addition of angular momenta, though somehow without reference to the orthogonal or Lorentz groups. Topics include the uncertainty principle, time evolution operators, Ehrenfest's theorem, and the correspondence principle connecting quantum and classical mechanics.
Lecture 8 Top13:00-15:00 Thur. 16th Mar. 2023
Please remember that this one will be online! -- (and it was online!)
Review session covering advanced quantum mechanical concepts. Squeezed states of the quantum harmonic oscillator, exploring minimum uncertainty states and coherent state transformations. Anisotropic quartic potential as a non-trivial example of perturbation theory. Angular momentum operators as the infinitesimal generators of spatial rotations, connecting to Lie group theory and the fundamental symmetries of quantum mechanics.
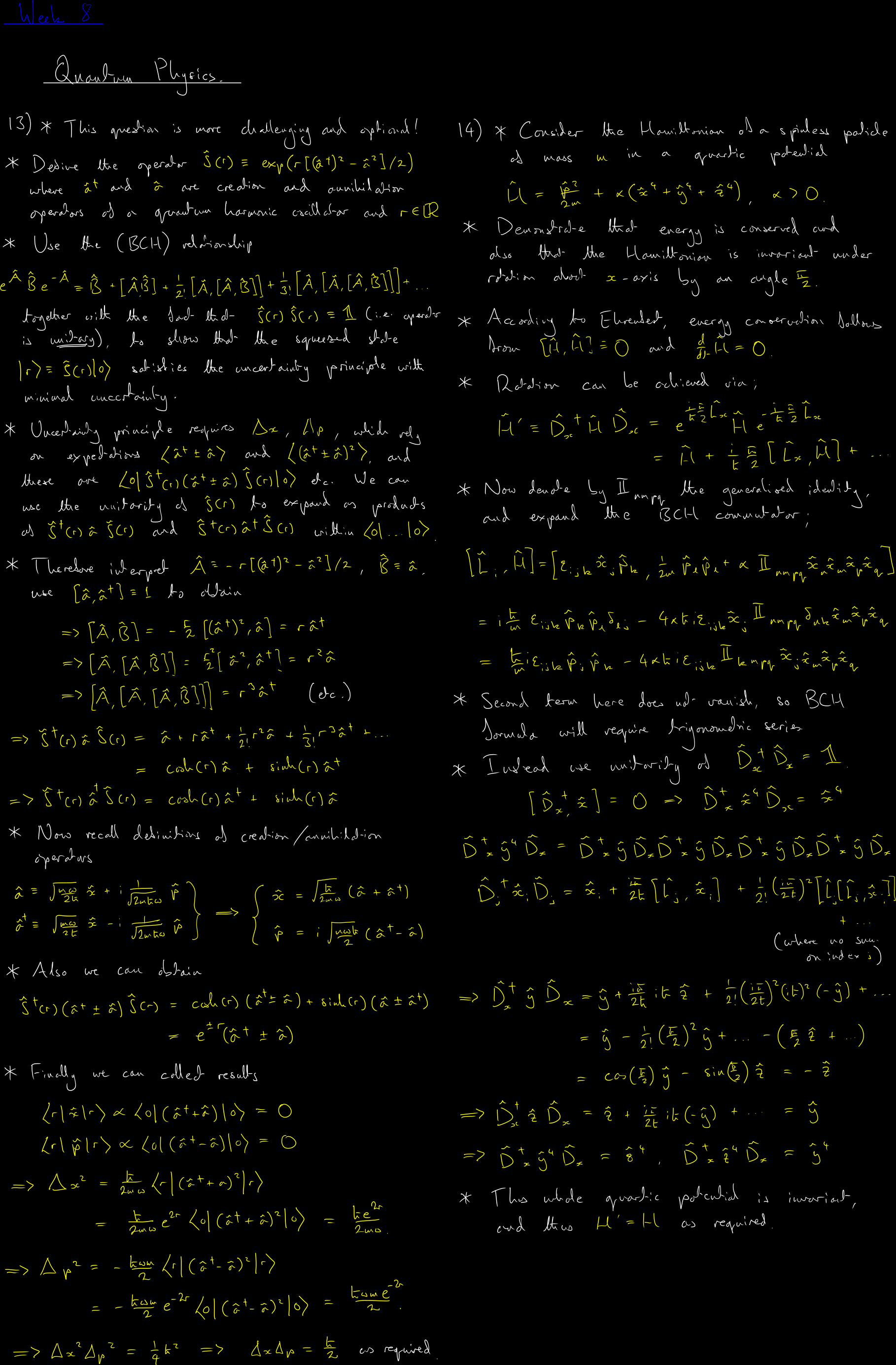
Lecture 7 Top14:00-16:00 Thur. 9th Mar. 2023
Please remember that this one will be online! -- (and it was online!)
Review session exploring measurement theory and advanced harmonic oscillator states. Prompt measurements of incompatible observables in succession, examining the fundamental limitations imposed by the uncertainty principle and non-commuting operators. Baker-Campbell-Hausdorff formula for operator exponentials and its applications to quantum dynamics. Coherent states of the quantum harmonic oscillator as eigenstates of the creation and annihilation operators with complex eigenvalues, displaying minimum uncertainty and classical-like behavior. These states bridge quantum and classical mechanics, maintaining their coherence under time evolution.

Lecture 6 Top14:00-16:00 Thur. 2nd Mar. 2023
Quantum spin, total angular momentum and Clebsch-Gordon coefficients, generation of spin, orbital and total angular momentum multiplets by raising and lowering, Stern-Gerlach apparatus, pure multi-particle states and the (non-relativistic limit of the) spin statistics theorem, degeneracy.

Lecture 5 Top14:00-16:00 Thur. 23rd Feb. 2023
Spherical polar coordinate basis for angular momentum operators, angular momentum ladder operators, orbital angular momentum and azimuthal quantum numbers, orbitals of a hydrogen-like atom, expected positions and distributions of the electron, spherical harmonics, separable Hamiltonia, higher-dimensional quantum harmonic oscillator, generalised conjugate quantum numbers and the symplectic form.

Lecture 4 Top14:00-16:00 Thur. 16th Feb. 2023
Changes of basis in the quantum Hilbert space, time evolution of non-stationary states and the expectation values of operators which are not compatible with the Hamiltonian. Creation and annihilation operators in the context of the quantum harmonic oscillator, Ehrenfest's theorem in the Schrödinger picture, time evolution operator, angular momentum operator. Hamiltonian dynamics and canonical quantisation, Groenwold's theorem.
Lecture 3 Top14:00-16:00 Thur. 9th Feb. 2023
Further discussion of quantum wells for the non-relativistic single particle, exploring tunneling through finite barriers and the conditions for bound state formation. Existence criteria for bound states based on potential depth and width. Quantum harmonic oscillator and the classical limit, demonstrating the correspondence principle through large quantum number behavior. Linear operators as quantum operators, establishing the mathematical framework for observables and their eigenvalue problems. The parity operator and discrete symmetries in quantum mechanics. Hermitian operators and their role in ensuring real eigenvalues for physical observables. Equivalence of position and momentum representations of the momentum operator, illustrating the dual nature of quantum descriptions, and polynomials constructed from the momentum operator showing the algebraic structure underlying quantum mechanics.

Lecture 2 Top14:00-16:00 Thur. 2nd Feb. 2023
Ideal square wells (finite and infinite), demonstrating particle-in-a-box quantization and energy level discretization. Continuity and boundary conditions for the wave function, exploring how physical constraints lead to quantized solutions. Probability current in one spatial dimension and the conservation of probability, connecting to classical current density. Correspondence principle showing how quantum mechanics reduces to classical mechanics in appropriate limits. Classical versus quantum expectation values, illustrating the probabilistic nature of quantum measurements and the emergence of classical determinism from quantum statistics.
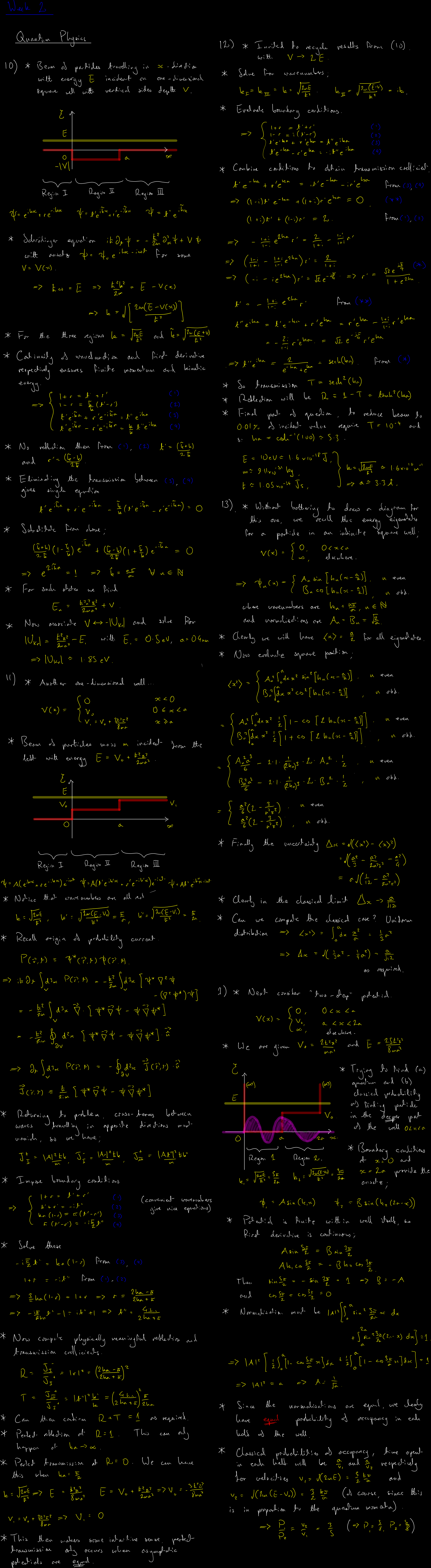
Lecture 1 Top14:00-16:00 Thur. 26th Jan. 2023
Photoelectric effect as historical evidence for quantum mechanics, demonstrating energy quantization and wave-particle duality. Application of Heisenberg uncertainty principle to classical mechanics, showing fundamental limits to simultaneous measurement precision. Bohr's quantisation criterion and the fine structure constant, connecting atomic structure to fundamental constants. Wave function normalisation as a probabilistic interpretation requirement. Non-relativistic massive particle dispersion relations, relating energy, momentum, and mass. The momentum operator and its representation in position space through differential operators. The mock exam from Jan. 18th is also discussed, providing practical application of these fundamental concepts.
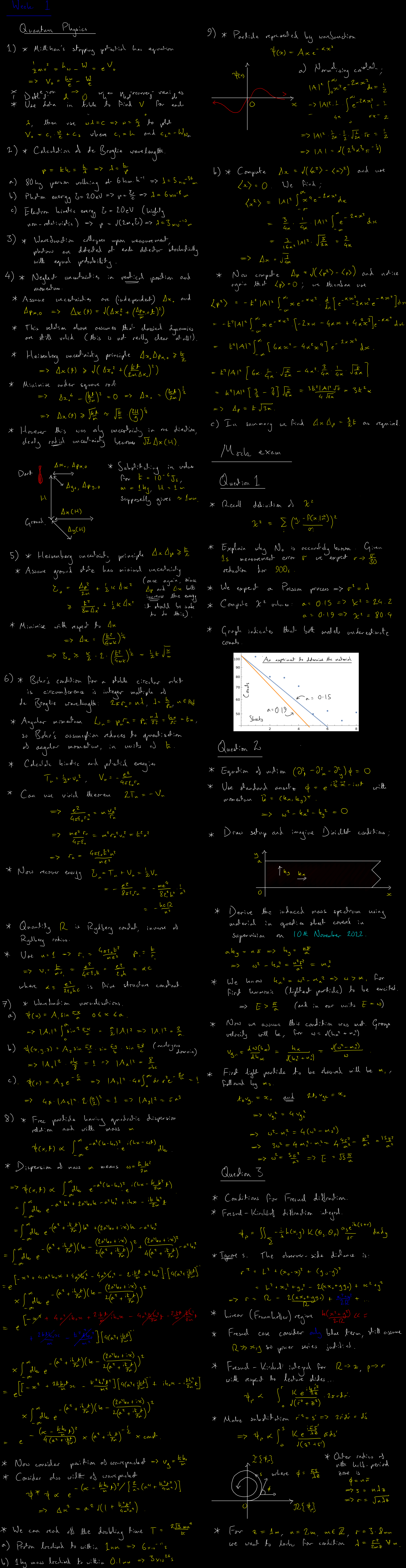
Oscillations, Waves and Optics Top
The "Oscillations, waves and optics" course is a strangely-constructed course designed to bridge the gap for second-year undergraduates who are about to learn quantum mechanics, introducing crucial mathematical techniques disguised as classical physics. There are two very important things which are introduced in disguise, namely hyperbolic systems and dispersion, which will prove essential for understanding quantum wave packets and relativistic field equations. The course covers driven harmonic oscillators, response functions, Q-factors and resonance phenomena before progressing to wave propagation in continuous media. String waves, acoustic waves, and electromagnetic wave optics are explored through boundary conditions, impedance matching, and junction problems. Diffraction theory emerges through the Fresnel-Kirchhoff integral, Fraunhofer and Fresnel approximations, leading to discussions of Airy disks, Rayleigh criteria, and resolution limits. Phase and group velocity concepts prepare students for quantum dispersion relations, while Fourier transforms connect classical optics to quantum wavefunction analysis. The small "Experimental methods" course is taught interstitially with this content, covering operational amplifiers, error analysis, and statistical data treatment including Poisson and Gaussian distributions.
Have a great Christmas break, everyone! Top

Lecture 8 Top14:00-16:00 Thur. 1st Dec. 2022
Fresnel plates and half-period zones, Fourier transform spectroscopy, convolution theorem and fringe visibility, Bayes' theorem, chi-squared, Gaussian and Poisson distributions.
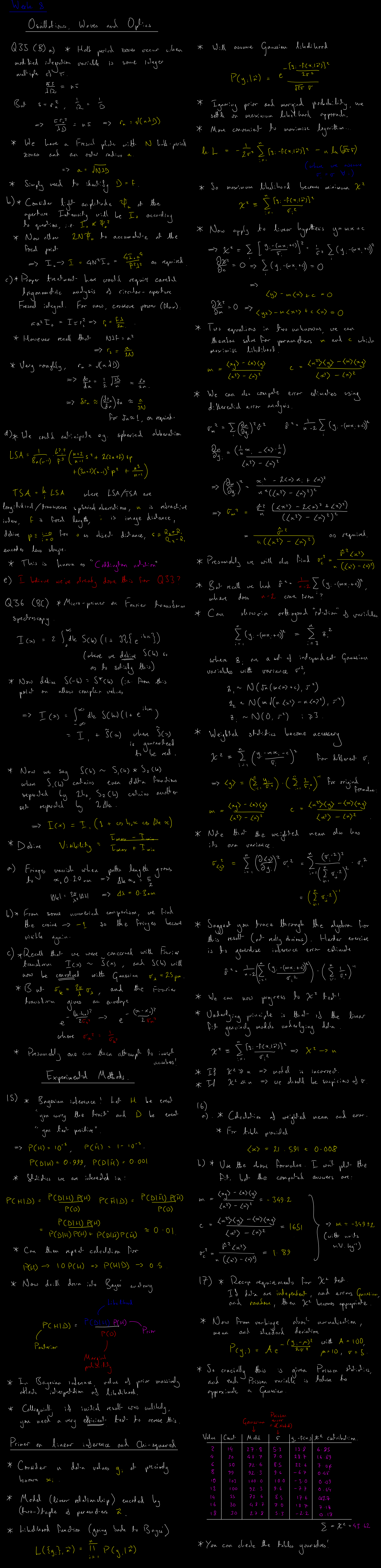
Lecture 7 Top14:00-16:00 Thur. 25th Nov. 2022
Fresnel diffraction regime from the Fraunhofer construction, Fresnel integral functions, Fresnel diffraction from a circular aperture, the Airy disk, Rayleigh's criterion for resolution, Poisson's spot, primer on probability distributions and variance, Poisson processes and shot noise.

Lecture 6 Top14:00-16:00 Thur. 17th Nov. 2022
Please remember that this one will be online! -- (and it was online!)
Calculation of Fraunhofer diffraction patterns from two-dimensional apertures, separation of scales and Fourier transforms, the effect of phase shifts in the aperture function, one-dimensional fringes and criteria for visibility, natural line width, pressure broadening and Doppler broadening, the Lorentzian and Gaussian line shapes, binning and quantized sampling.

Lecture 5 Top14:00-16:00 Thur. 10th Nov. 2022
Dispersion of a relativistic massive particle (extra example content), complementary phase and group velocity, energy and the speed of light, why the rectangular elastic waveguide is a model for this, mass quantization and evanescent modes, introduction to the Fresnel-Kirchhoff diffraction integral, the Fresnel approximation, the Fraunhofer approximation, and the Fourier transform of a rectangular aperture, differential error analysis and sub-Nyquist sampling.

Lecture 4 Top14:00-16:00 Thur. 3rd Nov. 2022
Phase velocity and group velocity derived from the Taylor expansion of the dispersion relation and the Fourier transform of the wave function, dispersion example in gravity waves (on water) examples of one-dimensional diffraction gratings, the relaxation oscillator circuit, random and systematic errors.

Lecture 3 Top14:00-16:00 Thur. 27th Oct. 2022
Junction conditions for waves in one dimension, impedance, reflection and transmission coefficients, example of sound, isothermal and adiabatic processes, the acoustic impedance, the acoustic wave equation, transverse string waves with point masses at junctions, the non-ideal operational amplifier.

Lecture 2 Top14:00-16:00 Thur. 20th Oct. 2022
String waves with position-dependent tension, exploring how varying mechanical properties affect wave propagation and reflection. Waves in solids and Young's modulus, connecting elastic properties to wave speeds in bulk materials. Dissipative terms in the wave equation, introducing energy loss mechanisms and their effects on wave amplitude and dispersion. Operational amplifiers as measurement apparatuses, covering ideal op-amp behavior and practical limitations in experimental setups. We did not complete a discussion of the "shunt" modification to ameliorate the low-frequency saturation of the integrator, which remains for future consideration.

Lecture 1 Top14:00-16:00 Thur. 13th Oct. 2022
Repeat: 15:30-18-30 Tue. 17th Oct. 2023
Oscillating systems and their mathematical description using complex notation for sinusoidal motion. Response functions for driven oscillators, exploring the frequency-dependent behavior of mechanical and electrical systems. Power transfer mechanisms and efficiency in oscillatory systems. Q-factor as a measure of oscillator quality and energy dissipation rates. Amplitude, velocity and acceleration response curves, demonstrating the phase relationships between driving forces and system response. Resonance phenomena and the dramatic enhancement of response at natural frequencies, with applications to mechanical vibrations and electrical circuits.

2022 mock exam Top
Two of the questions are copied from Tripos papers, one is sprinkled in for extra seasoning.
The blackboard from the post-mock session.

Methods in Theoretical Physics Top
The "Methods" were meant to be a series of informal discussions within the research group during the period where we had some great summer students with us, covering advanced topics in theoretical physics beyond the standard undergraduate curriculum. They tailed off after only a few weeks, but could perhaps be revivified in 2023 if someone wants to contribute content? The series explored sophisticated mathematical techniques including constrained Hamiltonian mechanics, Dirac brackets for gauge theory quantization, conformal field theory methods, and the Virasoro algebra as a central extension of conformal transformations. Topics included first-class versus second-class constraints, highest weight representations, central charges in two-dimensional CFTs, and the distinction between Einstein and Jordan frames in scalar-tensor theories of gravity. These advanced methods bridge undergraduate physics with cutting-edge research topics in string theory, general relativity, and quantum field theory.
Lecture 4 Top
Conformal transformations in general relativity. The Einstein frame versus Jordan frame formulations of scalar-tensor theories. Physical interpretation of different conformal frames and their observable consequences.

Lecture 3 Top
Introduction to conformal field theory. Conformal transformations and their generators. Scale invariance and the conformal group in various dimensions. Applications to critical phenomena and string theory.
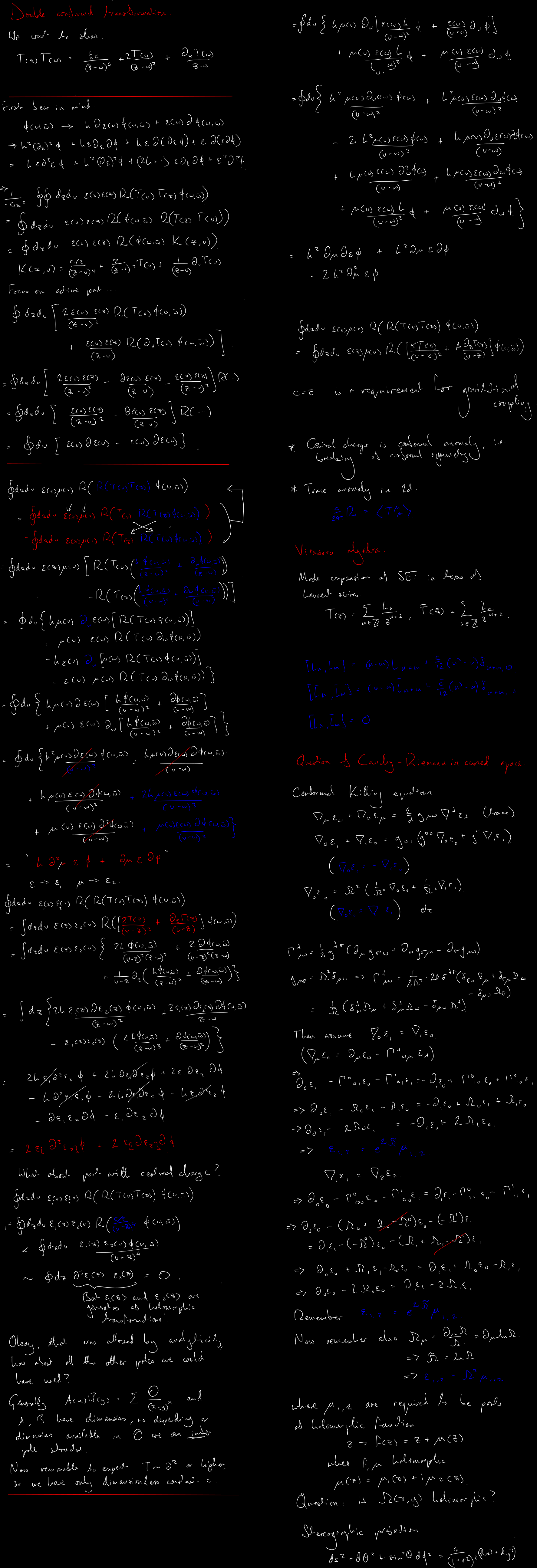
Lecture 2 Top
The Virasoro algebra as the central extension of the Witt algebra. Generators of conformal transformations in two dimensions. Central charge and its physical significance. Representations and highest weight states.


Lecture 1 Top
Hamiltonian formulation of constrained systems. Primary and secondary constraints. First-class and second-class constraints. Dirac brackets and the canonical quantization of gauge theories. Examples from classical mechanics and field theory.

Relativistic Astrophysics and Cosmology Top
The "Relativistic astrophysics and cosmology" course is the Physics Department's idea of applied relativity, presented to fourth-year undergraduates and covering the modern interface between general relativity and observational astronomy. There are some good patches in the course, which was first constructed many years ago, and it is now improving with continued efforts by Dr. Handley. The course explores gravitational wave astronomy, deriving chirp masses and inspiral dynamics for binary systems detected by LIGO/Virgo. Gravitational lensing is treated through the thin lens approximation, Einstein rings, and weak lensing techniques. Cosmological applications include the Friedmann equations for expanding universes, distance-redshift relations, the virial theorem for bound systems, and the observable signatures of quasars at high redshift. Topics connect relativistic physics to real astrophysical phenomena including black hole mergers, cosmic expansion, dark matter, and the early universe. The course bridges theoretical general relativity with practical data analysis techniques used in modern cosmological surveys and gravitational wave detection.
Lecture 4 Top
Virial theorem and its applications to gravitationally bound systems. Observable signatures of quasars embedded in an expanding universe, including redshift effects and luminosity distance relations. Angular diameter distance and the peculiar behavior at high redshifts. Extensive manipulation and derivation of the Friedmann equations governing cosmic expansion.

Lecture 3 Top
Gravitational waves and binary inspirals, deriving the chirp mass for equal-mass binary systems. Gravitational lensing construction using the thin lens approximation, Einstein rings and their formation conditions. Cosmological redshift in expanding spacetime. Particle horizon, Hubble horizon, and the observable universe - exploring causal structure and cosmic event horizons in expanding cosmologies.

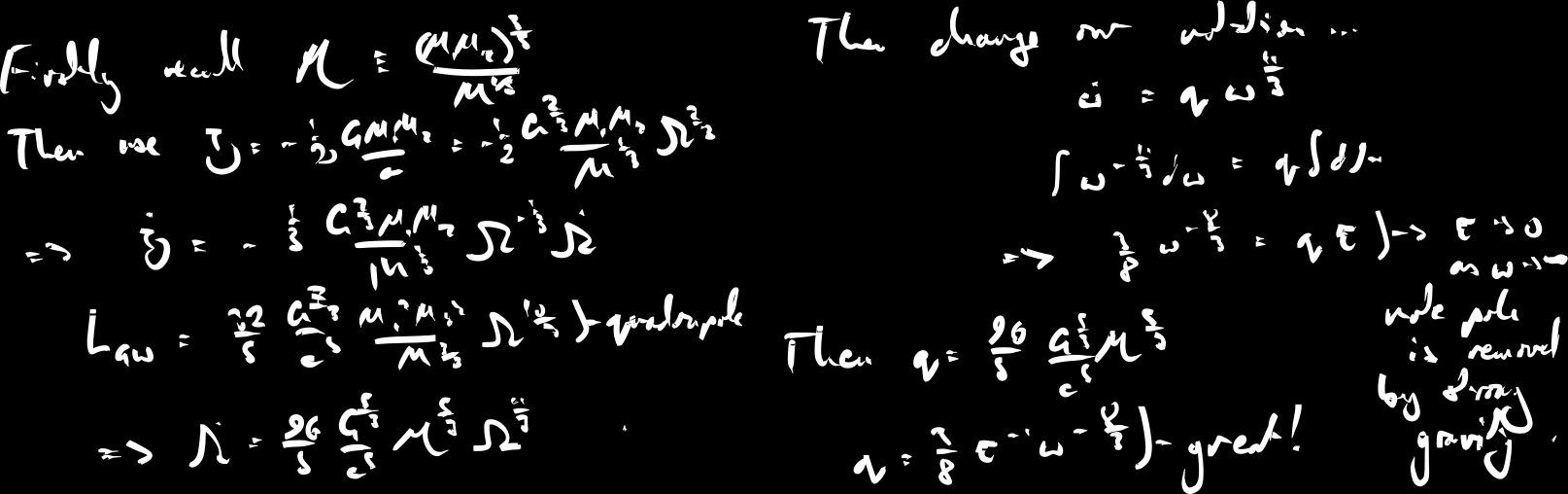
Supplementary calculation of optical depth in cosmological contexts: